I want to find the rational numbers $a$, $b$, $c$ satisfying the condition
$$\displaystyle \int _ { 5 } ^ { 21 } \frac { \mathrm { d } x } { x \cdot \sqrt { x + 4 } } = a \ln 3 + b \ln 5 + c \ln 7.$$ I solve by hand.
Integrate[1/(x Sqrt[x + 4]), {x, 5, 21}]
1/2 Log[15/7]
From here, I got, $ a = \dfrac{1}{2} $, $ b = \dfrac{1}{2} $, $ c = -\dfrac{1}{2} .$
How can I tell Mathematica to do that?
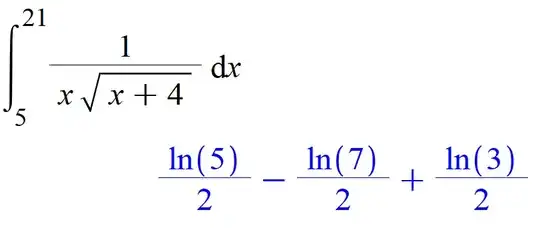

Integrate[1/(x Sqrt[x + 4]), {x, 5, 21}] // PowerExpand // Expand. – xzczd Feb 12 '19 at 08:46