I want to solve the telegraph equation with a spatial discretization forced at 200 points. I tried:
reg = Line[{{0}, {1}}];
shape = Cos[16 π (x - 0.5)] D[0.125 Erf[(x - 0.5)/0.125], x];
op = D[u[t, x], {x, 2}] - D[u[t, x], {t, 2}];
ics = {u[0, x] == shape, Derivative[1, 0][u][0, x] == 0};
sol = NDSolveValue[{op == 0, ics}, u, {t, 0, 2}, {x} ∈ reg, MaxStepSize -> 0.005];
Plot[shape, {x, 0, 1}, PlotRange -> All,Frame -> True]
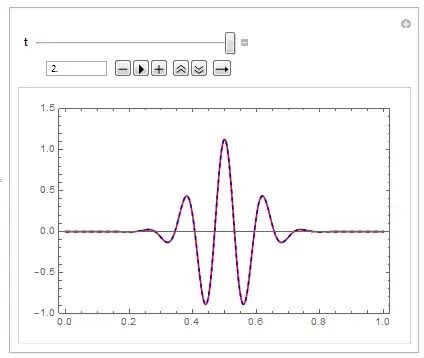
Plot[sol[0, x], {x, 0, 1}, PlotRange -> {-1, 1.5}, Frame -> True]
The plots show that NDSolve has chosen 20 spatial points. My MaxStepSize option is used for the temporal variable t and not for the spatial variable x.
What is the
NDSolveoption or syntax for forcing 200 spatial points?Where is this information in the
NDSolvedocumentation?Is there a
NDSolvemethod that would have by default discretize more cleverly?
Edited question given the first answers that were posted:
- How to force the initial spatial meshing at 200 points, keeping the region specification for x and consequently the finiteElement method ?

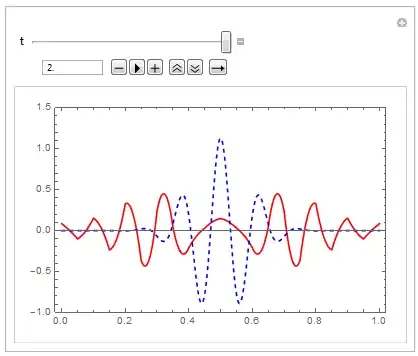
NDSolvebyNDSolveValuewouldn't help at all. – andre314 Feb 13 '19 at 20:29