6
LatticeData["SimpleCubic", "Image"]

The above line gives me a single cube (2 lattice points in each direction).

But I want a lattice with 4 lattice points in each direction. How do I generate that?

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
PyariBilli
  • 163
  • 1
  • 3

2 Answers2

12

The comments I got for this post are about speed basically. I improved it greatly because I removed opacity objects (which are nice visually but cause slow down). So let me just show the final result of fast and much more complicated (Tetrahedral) lattice than yours (which means your simple cubic will work too but with a bonus). So get your data

cell = LatticeData["TetrahedralPacking", "Image"];

Build extended lattice:

Graphics3D[Translate[DeleteCases[cell, {_, _, Polygon[_]}, Infinity][[1]], 
  2 Tuples[Range[3], 3]], Boxed -> False]

enter image description here

Now, let me go back in time and explain from the very beginning how it works. A brute force approach. Here is a single lattice cell:

cell = LatticeData["SimpleCubic", "Image"];

Now use Translate:

Graphics3D[Translate[cell[[1]], 2 Tuples[Range[4], 3]], Boxed -> False]

enter image description here

Even so the method is a bit wasteful (you repeating overlapping spheres), it is very simple and works for much more complicated crystal structures where creating custom grid is tedious - plus the style of lattice data is nice:

cell = LatticeData["TetrahedralPacking", "Image"]

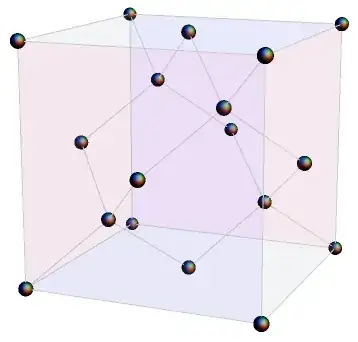
enter image description here

Graphics3D[Translate[cell[[1]], 2 Tuples[Range[2], 3]], Boxed -> False]

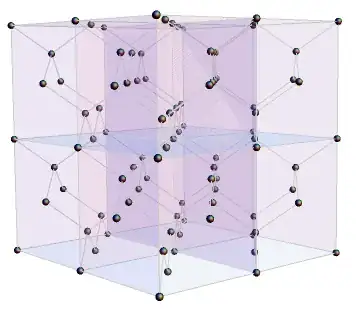
enter image description here

Vitaliy Kaurov
  • 73,078
  • 9
  • 204
  • 355
5

It is easy to generate coordinates for these using Tuples:

coords = Tuples[Range[4], 3]

Graphics3D@Point[coords]

Mathematica graphics

If you need the grid lines too, you can generate a 2D lattice for each face in a similar way and extrude them into lines.

Szabolcs
  • 234,956
  • 30
  • 623
  • 1,263
  • Is there a way in which i can connect those dots and replace the dots by spheres. – PyariBilli Feb 06 '13 at 16:37
  • @gforce89 Yes. Just use Sphere[#, radius]& in place of Point. For the lines you need to generate a 2D grid for each face. – Szabolcs Feb 06 '13 at 16:38
  • 2
    what i finally used was this : tpls = Tuples[Range[4], 3]; lines3 = Table[Partition[RotateRight[#, k] & /@ tpls, 4], {k, 0, 2}]; Graphics3D[{{RGBColor[#], Sphere[#, 1/10]} & /@ tpls, Tube /@ lines3}, Boxed -> False] – PyariBilli Feb 06 '13 at 16:42