Is there a way to draw a level tree?

Question

Consider the following expression.

expr = {a, {b1, b2}, {c, {d1, d2}}};

One can get the levels in an expression as follows:

ClearAll[levels];
SetAttributes[levels, {HoldAllComplete}];
levels[expr_] := 
  Column @ Table[Level[expr, {level}, Heads -> True], {level, 0, Depth[expr]-1}];
levels[expr]

But when I look at the TreeForm of it expr

TreeForm[expr]

I don't see what I expected: the leaf count for this expression should be 10.

LeafCount[expr]

One can try to get the true level tree as follows:

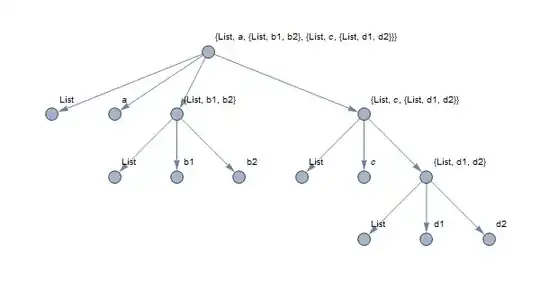
Graph[
  {
    Sequence @@ (expr\[UndirectedEdge]#& /@ {List, a, {b1, b2}, {c,{d1, d2}}}),
    Sequence @@ (expr[[2]]\[UndirectedEdge]#& /@ {List2, b1, b2}),
    Sequence @@ (expr[[3]]\[UndirectedEdge]#& /@ {List3, c, {d1, d2}}),
    Sequence @@ (expr[[3,2]]\[UndirectedEdge]#& /@ {List4, d1, d2})
  }, VertexLabels -> "Name"]

Is there a way to produce this graph for arbitrary expression?

Also, multiple vertices with the same name List get joined so I have to rename them to List1, List2, ..., etc. Is there a way to fix this while keeping the layout of the graph? ` asically, I want to display heads at the same level as their parts, which is their true position in the tree.

Answer 1

GraphComputation`ExpressionGraph[expr /. List -> (List[List, ##] &)]

TreeForm[expr /. List -> (List[List, ##] &)]

rules = List @@@ SparseArray`ExpressionToTree[expr /. List -> (List[List, ##] &)];
edges = DirectedEdge @@@ (rules[[All, All, 2]] + 1);
vertices = Property[#2 + 1, {VertexLabels -> #3}] & @@@ DeleteDuplicates[Flatten[rules, 1]];

TreeGraph[vertices, edges, ImagePadding -> 40, ImageSize -> 600,  VertexSize -> Medium]

Update: An alternative approach is to use the original expression with ExpressionToTree and add new edges:

g1 = Graph[SparseArray`ExpressionToTree[{a, {b1, b2}, {c, foo[d1, d2]}}], 
  VertexLabels -> "Name", VertexLabelStyle -> 14, ImageSize -> 600]

newedges = # \[DirectedEdge] 
    {Symbol[ToString[Head[First@Last[#]]] <> ToString[#[[2]]]]} & /@ 
   Select[VertexList[g1], Head[#[[1]]] === Symbol &];
VertexReplace[EdgeAdd[g1, newedges], v_ :> Last[v]]

Answer 2

Try the code

levelTree[expr_] := Replace[expr, {h_[x___] -> {h, x}}, {0, Infinity}];    
levelTree @ {a, {b1, b2}, {c, {d1, d2}}}    

which returns

{List, a, {List, b1, b2}, {List, c, {List, d1, d2}}}

A simple exmaple

levelTree[a b + c d]

which returns

{Plus, {Times, a, b}, {Times, c, d}}

I like the lispy variation

levelTree[expr_] := Replace[expr, (h : Except[List])[x___] -> {h, x}, {0, Infinity}];
levelTree @ plus[car[{1, 2}], cdr[{3, 4}]]

which returns

{plus, {car, {1, 2}}, {cdr, {3, 4}}}

Given any of these results, you can now use TreeForm[] or ExpressionGraph[] or some other custom Graph display.