4

I need to find the area distribution function of the 2D Voronoi cells in Mathematica version 11 and later. My old instructions for Mathematica 9 don't work anymore. How can I do it?

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
massimo
  • 41
  • 2

2 Answers2

9

Crossposted and much more extended discussion here (see comments):

https://community.wolfram.com/groups/-/m/t/1620190

I think it is a GammaDistribution and we can show it, see also this paper by Tanemura.

@C.E.'s answer is a good start, but without careful consideration, it might yield wrong stats. To gather good statistics, let's build a "large", 5000 cells VoronoiMesh within a unit Disk:

pts = RandomPoint[Disk[], 5000];
mesh = VoronoiMesh[pts, Axes -> True]

We see the stats are obviously offset by the presence of "border" cells of much larger area than regular inner cells have.

enter image description here

Let's exclude large cells by selecting only those within original region of random points distribution - unit Disk:

vor=MeshPrimitives[mesh,2];
vor//Length

5000

vorInner=Select[vor,RegionWithin[Disk[],#]&];
vorInner//Length

4782

We got fewer elements of course and they all are nice regular cells:

Graphics[{FaceForm[None], EdgeForm[Gray], vorInner}]

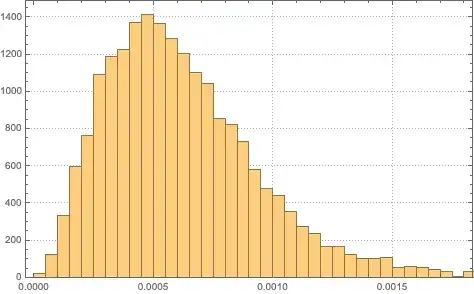
enter image description here

Now you can see that there is a minimum of distribution at zero area. Close to zero-area cells of course are not present much with the finite number of points per region (or finite density). So there is some prevalent finite mean area there. 

areas = Area /@ vorInner;
hist = Histogram[areas, Automatic, "PDF", PlotTheme -> "Detailed"]

enter image description here

You can find a very close simple analytic distribution:

dis=FindDistribution[areas]

GammaDistribution[3.3458431368450587,0.00018456010158014188]

which matches very nicely the empirical histogram:

Show[hist, Plot[PDF[dis, x], {x, 0, .0015}]]

enter image description here

And now it is easy to find thing like:

{Mean[dis], Variance[dis], Kurtosis[dis]}

{0.0006175091492073445, 1.1396755130437449*^-7, 4.793269963533813`}

Probability[x > .0005, x \[Distributed] dis]

0.5740480899719699`

Vitaliy Kaurov
  • 73,078
  • 9
  • 204
  • 355
  • i used to avoid Histogram preferring BinCounts, in this way i could obtain a table and then his fit. is there a possibility to determine the values of the bars? – massimo Apr 05 '19 at 18:25
7

First compute the Voronoi mesh:

pts = RandomReal[{-1, 1}, {25, 2}];
mesh = VoronoiMesh[pts]

Mathematica graphics

Then compute the areas of the mesh primitives (MeshPrimitives yields a polygon for each Voronoi region):

areas = Area /@ MeshPrimitives[mesh, 2];
Histogram[areas]

Mathematica graphics

Decreasing effect of unbounded cells

As Vitaliy pointed out in his answer, there are unbounded cells in the Voronoi diagram. For example like this:

pts = RandomReal[{-1, 1}, {1000, 2}]
VoronoiMesh[pts]

Mathematica graphics

In this case, it works well to adjust the bounding box:

VoronoiMesh[pts, {{-1, 1}, {-1, 1}}]

Mathematica graphics

More generally, we might create a bounded Voronoi diagram with the methods described in Making a Voronoi diagram bounded by the convex hull.

Removing unbounded cells

Chip provided a way, in a comment here below, to remove unbounded cells. Note that some of the unusually large cells are bounded and will be kept.

(* Chip's code for finding the points belonging to unbounded cells. *)
toRemove = MeshCoordinates[RegionBoundary[DelaunayMesh[pts]]];

We can now find the area distribution of the remaining cells like this:

sel = Select[
   MeshPrimitives[mesh, 2],
   Not@*Or @@ RegionMember[#, toRemove] &
   ];
Area /@ sel

We can inspect the remaining polygons like this:

colors = RandomColor[Length[sel]];
Show[
 Graphics@Riffle[colors, sel],
 Graphics[{Red, Point[toRemove]}]
 ]

Mathematica graphics

C. E.
  • 70,533
  • 6
  • 140
  • 264
  • 1
    We can also query for the cell areas via PropertyValue[{mesh, 2}, MeshCellMeasure]. – Greg Hurst Feb 24 '19 at 18:42
  • This could give wrong stats, C.E. and @ChipHurst. I posted a bit different version. – Vitaliy Kaurov Feb 24 '19 at 19:18
  • @VitaliyKaurov Thanks, good observation. Now if only there was a simple way of selecting the unbounded elements and removing them... (Something to do with the boundary mesh?) – C. E. Feb 24 '19 at 20:14
  • @C.E. I believe the unbounded cells correspond to the nodes that lie on the boundary of the convex hull. – Greg Hurst Feb 24 '19 at 21:03
  • In fact to avoid the issue of collinear points, we can take the nodes to be from the Delaunay triangulation: MeshCoordinates[RegionBoundary[DelaunayMesh[pts]]];. – Greg Hurst Feb 24 '19 at 21:06
  • @ChipHurst Thanks, I posted a method based on this idea. – C. E. Feb 24 '19 at 21:47
  • RegionBoundary[DelaunayMesh[pts]] is just RegionBoundary[ConvexHullMesh[pts]], no? (Presumably, getting the convex hull takes less effort than a full triangulation.) – J. M.'s missing motivation Feb 25 '19 at 02:15
  • 1
    @J.M.iscomputer-less Mathematically yes, but there are contrived examples due to machine precision. For example Tally[Table[ Length[MeshCoordinates[ ConvexHullMesh[{{0, -1}, {0, 0}, {1, Sqrt[2]}, {#, # Sqrt[2]} &@ RandomReal[{1, 3}]}]]], 1000]] – Greg Hurst Feb 25 '19 at 02:24
  • @C.E. Note that the ones ‘we’d like to remove’ have finite area and should stay. – Greg Hurst Feb 25 '19 at 03:47
  • 1
    @ChipHurst I thought about that, but they are considerably larger than the other ones. Consider e.g. this. It could skew statistics like the mean. Also, Vitaliy removed all such cells in his answer. But I changed the sentence to be clearer. – C. E. Feb 25 '19 at 03:54