Is it possible to rotate the Isolines on a Surface Using `MeshFunction`?

Question

This came up in a different context but some expertise in 3D surfaces or the graphic options would be appreciated. I'm trying to extrapolate the curves from any given surface and things seem to be going quite smoothly. All the curves can be grabbed in one more step as a GraphicsComplex. Perfect for more processing. However, now I'm trying to rotate the isolines to get even more control. This is possible in other software but I'm not sure how it was achieved. I assume there is some way to use the MeshFunction to rotate the Mesh through at least 45 degrees but all my searching hasn't brought up anything helpful. A less practical approach might be to find the intersecting curve of a regularly spaced vertical planes.

Plot3D[Cos[(x y)/2], {x, 0, 4}, {y, 0, 8},
BoxRatios->{4,8,1},
Boxed->False,
Axes->False,
ImageSize->Large,
Mesh->{3,8},
PlotStyle->Directive[Lighting->"Neutral",FaceForm[White,Specularity[0.2,10]]]]

J. M.'s missing motivation · Accepted Answer · 2019-02-25T09:34:57.603

13

Since we have the identity

RotationMatrix[θ] == {AngleVector[-θ], AngleVector[π/2 - θ]}

one can use this to construct a mesh that is arbitrarily oriented; e.g.

Manipulate[Plot3D[Cos[x y/2], {x, 0, 4}, {y, 0, 8}, BoxRatios -> Automatic, 
                  MeshFunctions -> {AngleVector[-θ].{#, #2} &,
                                    AngleVector[π/2 - θ].{#, #2} &},
                  PlotStyle -> Directive[Lighting -> "Neutral",
                                         FaceForm[White, Specularity[0.2, 10]]]],
           {θ, 0, 2 π}]

Manipulate demo

Note that this rotates the mesh clockwise; use MeshFunctions -> {AngleVector[θ].{#, #2} &, AngleVector[π/2 + θ].{#, #2} &} instead if the anticlockwise version is desired.

edited Feb 25 '19 at 09:34

answered Feb 25 '19 at 06:55

J. M.'s missing motivation

124,525
11
401
574

(If anyone is kind enough to edit my post to include the resulting image, please do so.) – J. M.'s missing motivation Feb 25 '19 at 06:56
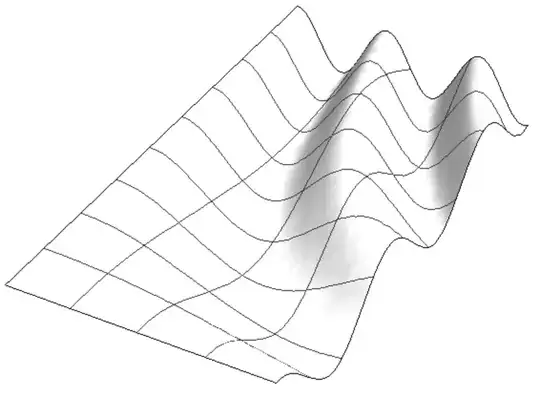
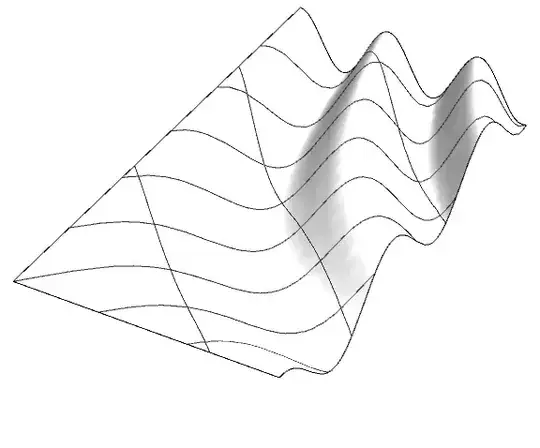
done (I took the liberty to replace the With with Manipulate to better show the advantages of this method) – Lukas Lang Feb 25 '19 at 08:40
Thanks a lot, @Lukas! The Manipulate[] is indeed much nicer. – J. M.'s missing motivation Feb 25 '19 at 09:31

kglr · Answer 2 · 2019-02-26T00:12:51.097

You can use MeshFunctions -> (Function /@ (RotationMatrix[θ].{#, #2})) to rotate by angle θ:

θ = 75 Degree;
meshfunctions = Function /@ (RotationMatrix[θ].{#, #2});

Plot3D[Cos[x y/2], {x, 0, 4}, {y, 0, 8}, 
 MeshFunctions -> meshfunctions, Mesh -> {3, 8},
 BoxRatios -> {4, 8, 1}, Boxed -> False, Axes -> False, 
 ImageSize -> Large, 
 PlotStyle -> Directive[Lighting -> "Neutral", FaceForm[White, Specularity[0.2, 10]]]]

For 45 Degree rotation you can use the simpler MeshFunctions -> {# + #2 &, # - #2 &} to get

Is it possible to rotate the Isolines on a Surface Using `MeshFunction`?

2 Answers2

Linked