Construct a section (or slice) through 3D Regions

Question

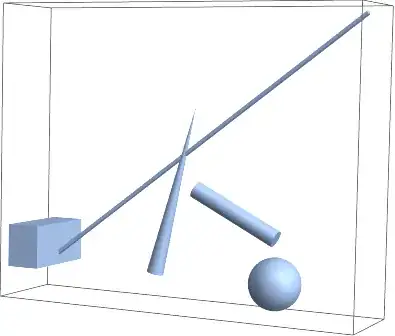
I would like to draw a section through some 3D regions. I start by making some simple 3D regions as a minimum working example.

gg = BoundaryDiscretizeGraphics[
     Graphics3D[#]] & /@ {Cuboid[{-0.2, -0.5, 0}, {0.2, 0.5, 0.5}], 
    Cone[{{1.5, 0, 0}, {2, 0, 2}}, 0.1] , 
    Cylinder[{{2, 0, 1}, {3, 0, 0.5}}, 0.1], Sphere[{3, 0, 0}, 0.3], 
    Tube[{{0, 0, 0}, {4, 0, 3}}, 0.03]};
rr = RegionUnion[gg, Boxed -> True]

Now I define an InfinitePlane that I would like to slice through my regions.

ip = InfinitePlane[{{0, 0, 0}, {4, 0, 0}, {4, 0, 1}}];
Show[
 Graphics3D[ip],
 Region[rr]
 ]

How do I get the 2D Region lying in the plane? Is this possible?

This post has an approach for 3D primitives but I can't see how to extend this to 3D regions.

Edit

@kglr suggest I can go further with ClipPanes. Here is his suggestion.

rc = RegionPlot3D[rr, ClipPlanes -> ip, 
  ClipPlanesStyle -> Opacity[0.1, Green]]

This does the slicing and shows the insides but does not give me 2D regions. Could this be a starting point?

Edit 2

Continuing to take instructions from @kglr (see comments). He suggests finding the intersection with the mesh primitives.

dg = DiscretizeGraphics@
  Quiet@Graphics3D[{DeleteCases[
      RegionIntersection[ip, #] & /@ 
       MeshPrimitives[rr, 
        2], _EmptyRegion | _Point | _RegionIntersection]}]

One can then extract the lines and reduce the coordinates to the values in the plane.

LL = MeshPrimitives[dg, 1] /. {a_, b_, c_} -> {a, c};
Graphics[LL]

This works. I will have to think further about what to do if the plane is not aligned with an axis. Reducing to 2D coordinates will then have to be done by a coordinate transform. However this is considerable progress and @kglr didn't have to post an answer!

Answer 1

Note that RegionIntersection[rr, ip] should give you what you want here but doesn't.

Since we have an axes aligned plane, we can workaround this by exploiting the second argument of DiscretizeRegion:

cut = DiscretizeRegion[RegionBoundary[rr], {{-0.2`, 4.1`}, {-0.5`, 0}, {-0.3`, 3.1`}}];

holes = FindMeshDefects[cut, "HoleEdges", "Cell"]["HoleEdges"];

slice = MeshRegion[MeshCoordinates[cut], holes, PlotTheme -> "Lines", 
  MeshCellStyle -> {1 -> Black}];

Show[slice, BoundaryMeshRegion[rr, BaseStyle -> Opacity[.3]]]

We can easily project to 2d as well:

BoundaryMeshRegion[MeshCoordinates[cut][[All, {1, 3}]], holes]

---

We can adapt this idea to any plane. I'll use HalfSpace to emphasize which side of the plane is kept.

halfSpaceClip[reg_, ___] /; !MeshRegionQ[reg] && !BoundaryMeshRegionQ[reg] && RegionEmbeddingDimension[reg] != 3 = $Failed;

halfSpaceClip[mr_, h_HalfSpace] /; RegionWithin[h, mr] := mr

halfSpaceClip[mr_, HalfSpace[n_, p_]] /; RegionWithin[HalfSpace[-n, p], mr] = EmptyRegion[3];

halfSpaceClip[mr_, HalfSpace[n_, p_]] :=
  Block[{rt, rot, bds, clip},
    rt = RotationTransform[{n, {0, 0, -1}}, p];
    rot = TransformedRegion[mr, rt];
    bds = RegionBounds[rot];

    clip = DiscretizeRegion[rot, {#1+5{-1,1}, #2+5{-1,1}, {p[[3]], #3[[2]]+5}}]& @@ bds;

    InverseTransformedRegion[clip, rt]
  ]

halfSpaceClip[___] = $Failed;

The same example:

cut = halfSpaceClip[RegionBoundary[rr], HalfSpace[{0, 1, 0}, {0, 0, 0}]];

holes = FindMeshDefects[cut, "HoleEdges", "Cell"]["HoleEdges"];

slice = MeshRegion[MeshCoordinates[cut], holes, PlotTheme -> "Lines", 
  MeshCellStyle -> {1 -> Black}];

Show[slice, BoundaryMeshRegion[rr, BaseStyle -> Opacity[.3]]]

A non axes aligned plane:

cut = halfSpaceClip[RegionBoundary[rr], HalfSpace[{.5, 1, -1}, {0, .5, .5}]];

holes = FindMeshDefects[cut, "HoleEdges", "Cell"]["HoleEdges"];

slice = MeshRegion[MeshCoordinates[cut], holes, PlotTheme -> "Lines", 
  MeshCellStyle -> {1 -> Black}];

Show[slice, BoundaryMeshRegion[rr, BaseStyle -> Opacity[.3]]]