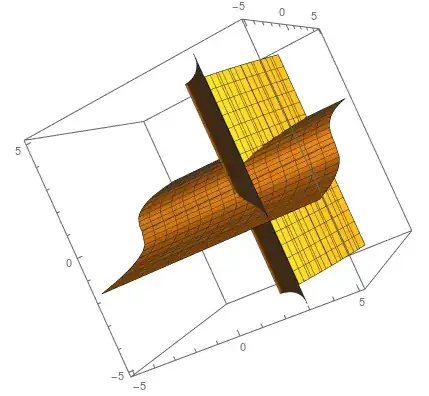
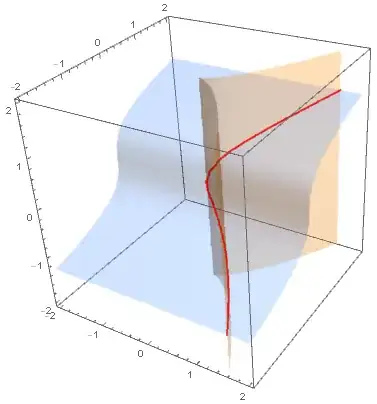
Suppose I have two nonlinear equalities $x^3 = y^2, y = z^3$. How can I visualize the manifold in $\mathbb{R}^3$ that is generated by simultaneously satisfying the two equalities? I think ContourPlot3D is the one to use but I couldn't get it to work show the set of points in $\mathbb{R}^3$ that satisfy the two equalities. The best I can do is make it show the intersection of the surfaces:
How can I plot the curve defined by the intersection in 3D?