Constructing a special square matrix

Question

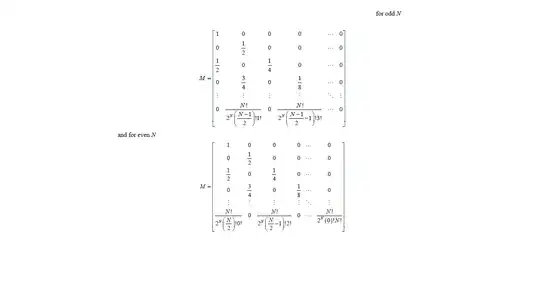
I am trying to define an $n \times n$ matrix for even $n$ using

d1 = 
 Table[
   Which[
     i < j, 0, i == j, i!/(2^i 0! i!), 
     EvenQ[i - j] && j == 0, (i)!/(2^i (i/2)! j!), 
     EvenQ[i - j] && OddQ[i], (i)!/(2^i ((i + 1)/2 - 1)! j!), 
     EvenQ[i - j] && EvenQ[i], (i)!/(2^i (i/2 - 1)! j!), 
     True, 0], 
   {i, 0, n}, {j, 0, n}]

Is my code correct? Will it be correct when $n$ is odd?

Probably you don't need a separate case for j==0. Also, is there are additional j dependencies in the other two cases (I don't know, because I don't know exactly what you are trying to do). What happens when n is odd? — mjw, Mar 01 '19 at 20:45
Okay, so i is the row, and j is the column, right? The term's dependence on j (other than whether it zero or not) is the j! in the denominator, yes? — mjw, Mar 01 '19 at 21:01
I am not sure that you would need a special case for j==0. Wouldn't it just follow the pattern also? Try n=4. Is this what you want (a few 3/4 over there in the lower left corner)? — mjw, Mar 01 '19 at 21:09
Dear mjw, I not sure if what I did is correct or not, that is why I need help...thanks — user62716, Mar 01 '19 at 21:11
How should we interpret the image you show? Is it the output are now getting or the output you want to get? — m_goldberg, Mar 02 '19 at 00:34
Also, don't use N as a variable. N is a reserved symbol for a built-in function. — m_goldberg, Mar 02 '19 at 00:40
Dear m_goldberg, N taking the values 2,4,6,8.....even,or 1,3,5,7,9...odd — user62716, Mar 02 '19 at 07:38
It would be very helpful if you could mention the book/paper/anything where these matrices are discussed. — J. M.'s missing motivation, Mar 02 '19 at 20:21
Also, it would be helpful if you state what exactly is the {i,j} entry of each matrix. — mjw, Mar 03 '19 at 01:55

Roman · Accepted Answer · 2019-03-03T03:47:51.377

1

This works for both even and odd $N$=n. Notice that the generated matrix is actually $(N+1)\times(N+1)$ as the indices run from 0 to $N$. You can see this in your images, which show an even-sized matrix for odd $N$ and vice-versa.

M[n_Integer /; n >= 0] :=
  SparseArray[{{i_,j_} /; EvenQ[i-j] && i>=j -> (i-1)!/(2^(i-1)((i-j)/2)!(j-1)!)},
    {n + 1, n + 1}]

If you need a non-sparse matrix, use Normal.

I'm not sure why the bottom-right matrix element in your odd-$N$ image is zero. Shouldn't it be $2^{-N}$ as it lies on the diagonal?

edited Mar 03 '19 at 03:47

answered Mar 03 '19 at 03:42

Roman

47,322
2
55
121

Or use // MatrixForm to view the matrix. – mjw Mar 03 '19 at 03:54
Dear all, many thanks for all comments, I will check and back...best regards – user62716 Mar 03 '19 at 20:08
Many thanks Roman, you solved my problem, thanks mjw – user62716 Mar 03 '19 at 20:30

mjw · Answer 2 · 2019-03-10T21:42:00.790

1

d1[n_] := Table[
            Which[i < j, 0,EvenQ[i - j], (i)!/(2^i ((i-j)/2)! j!), True, 0], 
                  {i, 0, n}, {j, 0, n}
               ]

The output seems to be what you want. Here are a couple of examples:

d1[3] // MatrixForm:

d1[4] // MatrixForm:

edited Mar 10 '19 at 21:42

answered Mar 03 '19 at 04:09

mjw

2,146
5
13

This is not the matrix from the images. In yours, element (3,1) is $3/8$ whereas in the original it is $3/4$. – Roman Mar 03 '19 at 06:19
Defining a matrix with MatrixForm is not a good idea as it interferes with subsequent calculations and confuses beginners. – Roman Mar 03 '19 at 06:19
You are right about the 3/4 vs 3/8. I"ll look at it again when I have some time. – mjw Mar 03 '19 at 13:45
Defining a matrix with MatrixForm... I did not know about the interference, please elaborate. I am also a beginner! – mjw Mar 03 '19 at 13:48
1

MatrixForm is only a display wrapper, like InputForm and TeXForm etc. If you define A={{1,1},{1,1}}//MatrixForm then a call like Eigenvalues[A] will fail because it is interpreted as Eigenvalues[MatrixForm[{{1,1},{1,1}}]] instead of Eigenvalues[{{1,1},{1,1}}]. Use MatrixForm only to display a matrix, not to define it. See https://mathematica.stackexchange.com/questions/3098/why-does-matrixform-affect-calculations – Roman Mar 03 '19 at 14:32
Yes, great point! I used MatrixForm here because I wanted to display the matrix. But you are right, I didn't consider later calculations. Edited use of MatrixForm to reflect your advice. Also, I've edited my answer after looking more carefully at the output. It's consistent with my point the other day that we only need one line to define the function. The 'one line' also ends up very similar to your definition (but with a different indexing). I guess there really is only one way (up to indexing) to define it. – mjw Mar 03 '19 at 14:44

Constructing a special square matrix

2 Answers2