Start with a quarter-circle of radius 1 centered at the origin and lying in the $xz$-plane:
arc = ParametricPlot3D[{Cos[t], 0, Sin[t]}, {t, 0, π/2}]
I want to dilate this by a factor of 2 and shift the center to {3, 0, 0}, then show the result graphically.
The following does not work:
shiftAndDilate3D = AffineTransform[{2 IdentityMatrix[3], {3, 0, 0}}]
Graphics3D[GeometricTransformation[arc3D, shiftAndDilate3D]]
The error I get is that Graphics3DBox is not a Graphics3D primitive or directive.
What am I doing wrong?
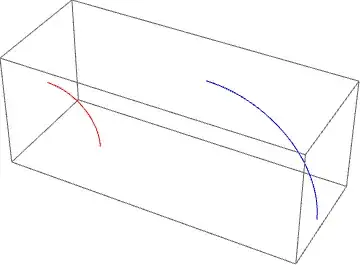
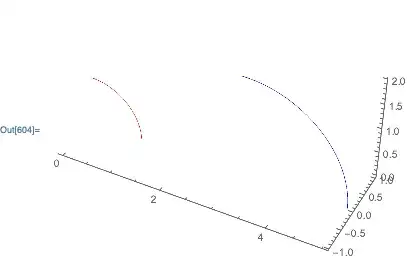
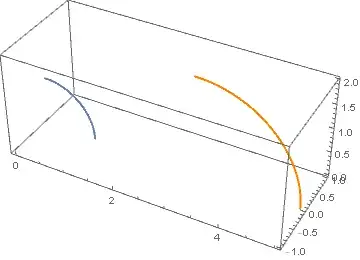
ParametricPlot3D[AffineTransform[{2 IdentityMatrix[3], {3, 0, 0}}] @ {Cos[t], 0, Sin[t]} // Evaluate, {t, 0, π/2}]. – J. M.'s missing motivation Mar 08 '19 at 01:46GeometricTransformation[]"; this list mixes up directives and primitives, so that doesn't count. – J. M.'s missing motivation Mar 08 '19 at 23:56