13

so this is currently what I'm building 

triangles[n_Integer?(# >= 2 &)] :=
  (*the subdivision by elementary geometry*)
  Flatten[ 
    Union[
      Table[
        Polygon[
          {{(i + j/2)/n, Sqrt[3]/2 j/n},
           {(i + 1 + j/2)/n, Sqrt[3]/2  j/n},
           {(i + 1/2 + j/2)/n, Sqrt[3]/2 (j + 1)/n}}],
        {j, 0, n - 1}, {i, 0, n - 1 - j}],
      Table[
        Polygon[
          {{(i + 1/2 + j/2)/n, Sqrt[3]/2 (j + 1)/n},
           {(i + 3/2 + j/2)/n, Sqrt[3]/2 (j + 1)/n},
           {(i + 1 + j/2)/n, Sqrt[3]/2 j/n}}],
        {j, 0, n - 1},{i, 0, n - 2 - j}]]]

(*Generate ternary frame*)
triangle = triangles[50];

(*acenters and acentroids match in this case*)
acoords = Table[triangle[[i]][[1]], {i, 1, Length[triangle]}];
acenters = Table[Mean[acoords[[i]]], {i, 1, Length[triangle]}];
acentroids = Table[RegionCentroid[triangle[[i]]], {i, 1, Length[triangle]}];

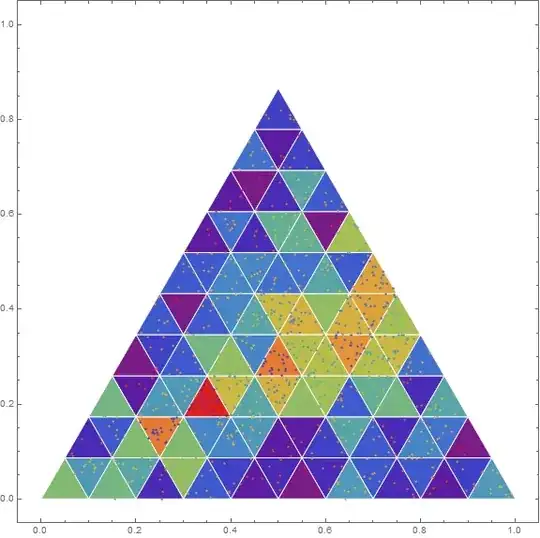
Using https://scicomp.stackexchange.com/questions/1473/sort-a-cloud-of-points-with-respect-to-an-unstructured-mesh-of-hexahedral-cells/1474#1474 I'm trying to recreate the following histogram module in R (https://stackoverflow.com/questions/26221236/ternary-heatmap-in-r):

cloud = RandomReal[{0, 1}, {1000, 2}];
indices = First /@ nf /@ cloud;
Histogram[indices];

tally = Tally[indices];

ListDensityPlot[Join[points, List /@ Sort[tally][[All, 2]], 2], 
  InterpolationOrder -> 0, 
  Epilog -> (Text[#2, points[[#1]]] & @@@ tally), 
  PlotRange -> {{-.5, 5}, {-.5, 5}}, Mesh -> All, 
  ColorFunction -> (ColorData["BeachColors"][1 - #] &)]

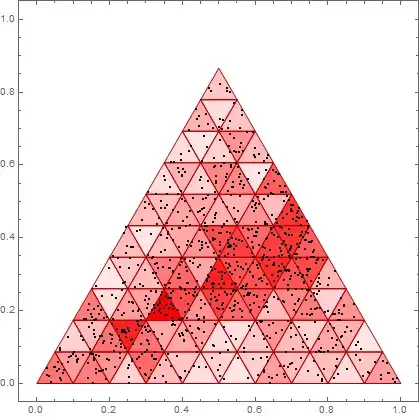
I think this will bin in hexagons, rather than triangles. Alternatively RegionMember might be the way

maps = Map[RegionMember, triangle];
counts = Table[Tally[Map[maps[[i]], cloud]], {i, 1, Length[maps]}]
m_goldberg
  • 107,779
  • 16
  • 103
  • 257
MKF
  • 591
  • 2
  • 10
  • 1
    Where is the definition on nf? And what is your question? – m_goldberg Mar 09 '19 at 14:42
  • nf = Nearest[N[points] -> Range@Length[points]];; I want to build the ternary plot as in https://stackoverflow.com/questions/26221236/ternary-heatmap-in-r – MKF Mar 09 '19 at 14:59
  • I spoke to Wolfram, they say RegionMember is computationally expensive, so I'm thinking of another way to check – MKF Mar 09 '19 at 16:48
  • 3
    Using maps[[i]] @ cloud instead of maps[[i]] /@ cloud will be orders of magnitude faster in the RegionMember approach. Of course using Nearest on the region centroids will be much faster than using RegionMember. – Carl Woll Mar 09 '19 at 17:36
  • Your definition o nf only begs the question — what is points. – m_goldberg Mar 10 '19 at 01:37
  • points can be replaced with acentres , please see @Szabolcs solution – MKF Mar 10 '19 at 02:17

1 Answers1

15
ClearAll[toSimplex, nF]
toSimplex = #[[1]] {1, 0} + #[[2]] {1, Sqrt@3}/2 &/@(Normalize[#, Total[#]/Max[#] &]&/@#)&;

n = 10;
centroids = N[RegionCentroid /@ triangles[n]];
nF = Nearest[centroids -> "Index"];

SeedRandom[1]
pts0 = RandomReal[{0, 1}, {1000, 2}];
pts = toSimplex @ pts0;
groups = GatherBy[pts, nF[#, 1] &];
tallies = {Rescale[Length /@ groups], triangles[n][[nF[#[[1]], 1][[1]]]] & /@ groups};
Show[Graphics[Transpose[{ColorData["Rainbow"] /@ #, #2} & @@ tallies], Frame -> True], 
 ListPlot[Tooltip[#, Length@#] & /@ groups, 
  PlotStyle -> (ColorData[{"Rainbow", "Reversed"}] /@ (tallies[[1]]))]]

enter image description here

Alternatively, you can use GeoHistogram which allows triangular bins:

Show[GeoHistogram[Reverse /@ pts, N[triangles[10]],
  ColorFunction -> "Rainbow", PlotStyle -> Directive[Opacity[1], EdgeForm[White]],
  PlotRange -> All, Frame -> True, GeoBackground -> None, 
  GeoRange -> {{0, 1}, {0, 1}} ], 
 ListPlot[Tooltip[#, Length@#] & /@ groups, 
  PlotStyle -> (ColorData[{"Rainbow", "Reversed"}] /@ (tallies[[1]]))], 
  PlotRange -> All, AspectRatio -> 1, ImageSize -> Large]

enter image description here

To color by opacity:

Show[GeoHistogram[Reverse /@ pts, N[triangles[10]], 
  ColorFunction -> (Opacity[Rescale[#, {0, 1}, {.1, 1}], Red] &), 
  PlotStyle -> EdgeForm[Darker @ Red], 
  PlotRange -> All, Frame -> True, GeoBackground -> None, 
  GeoRange -> {{0, 1}, {0, 1}}], 
 ListPlot[pts, PlotStyle -> Directive[PointSize[Small], Black]], 
 AspectRatio -> 1, PlotRange -> All]

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896