Update: Inspired by Henrik's answer, an alternative way to use SparseArray to construct the adjacency matrix directly:
nzp[n_] := SparseArray[{Band[{1, n + 2}, {n^2, n^2}] -> Join[ConstantArray[1, n - 1], {0}],
Band[{2, n + 1}, {n^2, n^2}] -> Join[ConstantArray[1, n - 1], {0}]}, {n^2, n^2}][
"NonzeroPositions"]
Graph[Range[8^2], UndirectedEdge @@@ nzp[8]]

And using the original grid layout (as suggested in Szabolcs's deleted answer):
Graph[Range[8^2], UndirectedEdge @@@ nzp[8], VertexCoordinates -> Tuples[Range@8, {2}]]

Update 2: If you have to work with GraphData[{"Bishop", {8,8}}] you can process its AdjacencyMatrix to delete the unwanted elements:
n = 8;
e = UndirectedEdge @@@ DeleteCases[
GraphData[{"Bishop", {n, n}}, "AdjacencyMatrix"][ "NonzeroPositions"],
{i_, j_} /; i > j || j > i + n + 2];
Graph[Range[n^2], e]
same picture as above
Original answer:
AdjacencyGraph[1 - Unitize[DistanceMatrix @ Tuples[Range@8, {2}] - Sqrt[2]]]
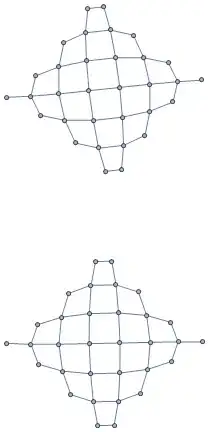
Also
RelationGraph[Sqrt[2] == EuclideanDistance @ ## &, Tuples[Range @ 8, {2}]]
same picture
RelationGraph[Abs[# - #2] == {1, 1} &, Tuples[Range@8, {2}]]
same picture



TransitiveReductionGraph, it is really meaningful only for directed graphs. For an undirected graph, it would be a simple spanning tree. You should also be aware that TransitiveReductionGraph is still buggy despite multiple requests to fix it during the past 4 years. Personally I am very frustrated with Wolfram Research's neglect ofGraphprocessing functions. – Szabolcs Mar 14 '19 at 12:22