Unexpected result from ArcLength

Question

I want to determine the arc lenght of a parametric curve $C: \{x(t),y(t) \} = \{ \cos(t)^p , \sin(t)^p \}$ with $p$ between $0$ and $1$, and $t$ between $0$ and $\pi/2$.

I set up the following function of $p$:

L[p_] :=  ArcLength[{Cos[t]^p, Sin[t]^p}, {t, 0, Pi/2}, 
                       Method -> {"NIntegrate", MaxRecursion -> 20}]

For $p=1$ we have a quarter of a circle of radius 1 and we know the arc length is equal to $\pi/2$. The above function gives the correct result: 1.5708.

For $p$ close to zero, the curve approaches a square, and we know the result should be very close to $2$. However, the function doesn't even come close to it. Evaluating L[1/100] results in 1.30603. Not close to 2 (it's not even bigger than Pi/2).

Plotting, results in the following:

Plot[L[p], {p, 0, 1}]

Any ideas? I'm running 11.0.0.0

Answer 1

Seems to be a precision thing.

L[p_] = {Cos[t]^p, Sin[t]^p}

ArcLength[L[1/100], {t, 0, π/2}, WorkingPrecision -> 1000]

1.99447959240474567...

Answer 2

I can only provide an alternative to bypass ArcLength.

The points pts of a quarter circle are scaled such that they lie on the desired curve; afterwards the length of the polygonal line is computed.

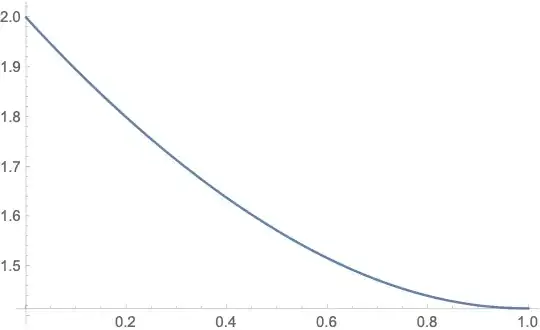
You will still get problems for values of p very close to 0, but at least you may obtain a qualitatively correct plot (so I hope).

Certainly this method won't provide you with the best possible accuracy. The relative error between the arclength $\ell$ of an arc and the length $s$ of a secant is roughly $|\ell/s - 1\| \leq \ell^2 \, \max(|\kappa|)$ in the limit of $\ell \to 0$. Here $\kappa$ denotes the curvature of the curve. Since the maximal curvature of the curve goes to $\infty$ for $p \to \infty$, the quality of this approximation will reduce significantly for $p \to 0$.

n = 10000;
pts = Transpose[{Cos[Subdivide[0., Pi/2, n]], Sin[Subdivide[0., Pi/2, n]]}];
L[p_] := With[{x = pts/Power[Dot[(Abs[pts]^(1/p)), {1., 1.}], p]},
  Total[Sqrt[Dot[Differences[x]^2, {1., 1.}]]]
  ]
Plot[L[p], {p, 0.001, 1}]

Edit

The ratio behind this is that in contrast to the parameterization

γ[t_, p_] = {Cos[t]^p, Sin[t]^p};

the parameterization

η[t_, p_] = {Cos[t], Sin[t]}/ Power[Cos[t]^(1/p) + Sin[t]^(1/p), p];

has finite speed which is always helpful for determining the arclength by integration:

assume = {p > 0, 0 < t < Pi/2};
speedγ[t_, p_] = Simplify[Sqrt[D[γ[t, p], t].D[γ[t, p], t]], assume];
speedη[t_, p_] = Simplify[Sqrt[D[η[t, p], t].D[η[t, p], t]], assume];
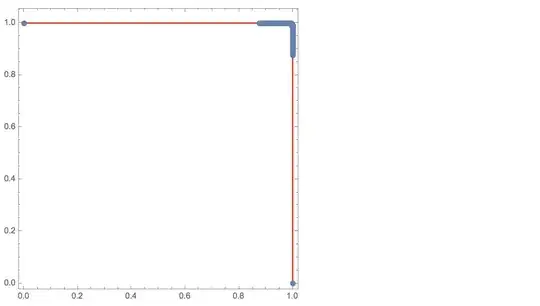
Quiet@GraphicsRow[{
   Plot[Evaluate[Table[speedγ[t, 2^-k], {k, 0, 10}]], {t, 0, Pi/2},
    PlotLabel -> "Speed of γ",
    PlotRange -> {0, 10}
    ],
   Plot[Evaluate[Table[speedη[t, 2^-k], {k, 0, 10}]], {t, 0, Pi/2},
    PlotLabel -> "Speed of η",
    PlotRange -> {0, 10}
    ]
   },
  ImageSize -> Large
  ]

Whit this parameterization, one can also employ NIntegrate to compute the arclength, at least for not too small p.

NIntegrate[speedη[t, 1/1000], {t, 0, Pi/2}]

2.

Answer 3

Manipulate[ParametricPlot[{Cos[t]^p, Sin[t]^p}, {t, 0, Pi/2}], {p, 0.01, 1}]

gives this plot at $p=0.01$:

(An unpreprocessing plot was here.)

UPDATE:

p = 0.01; ParametricPlot[{Cos[t]^p, Sin[t]^p}, {t, 0, Pi/2}, Axes -> False, Frame -> True, PlotRange -> {{0, 1.1}, {0, 1.1}}]

So yes, the sides are not shrinking, but Mathematica seems to be missing some of the curve ...

ADDITIONAL UPDATE:

f[t_][p_] := {Cos[t]^p, Sin[t]^p};
p = 0.01;
k = 10^6;
Show[
  ListLinePlot[Transpose@f[\[Pi]/(2 k) Range[0, k]][p], PlotStyle -> Red], 
  ListPlot[Transpose@f[\[Pi]/(2 k) Range[0, k]][p], PlotStyle -> PointSize[Large]], 
  AspectRatio -> 1, Frame -> True, Axes -> False
]

If we sample $t$ with one million equally spaced points, there are big jumps to the first and the last point!

Plot[f[10^-q][.01][[2]], {q, 0, 100}, Frame -> True, Axes -> False, FrameLabel -> {"-Log10[t]", "f[[2]]"}]

This plot shows that we need $t \le 10^{-100}$ for the $y$-value of the curve to be less than $\approx 0.1$ when $p=.01$.