1

I need to find all positive roots of the following transcendental equation

2*cot(x) = 6.4*x-0.1563/x

I know that the roots can be visualised as the intersecting point of the y=LHS and y=RHS curves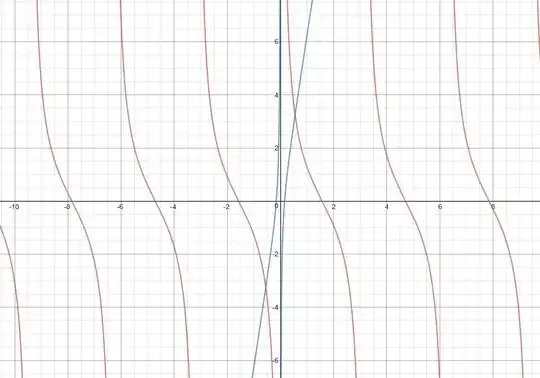enter image description here

Is there any way, I can obtain say the first 20 roots of this equation and obtain their values ?

enter image description here

Avrana
  • 297
  • 1
  • 4
  • 14
  • Please try the solutions in the linked thread, after simplifying your equation to $2x\cos x=(6.4x^2-0.1563)\sin x$. – J. M.'s missing motivation Mar 16 '19 at 06:37
  • Not quite a duplicate as in this case the roots are distributed very regularly, $x_n\approx (n - 1)\pi + 5/(16 \pi n)$, and a simple FindRoot can be used with this approximation as a starting point. In this way we're not missing any roots, even for very large $n$. – Roman Mar 16 '19 at 07:16
  • @Roman Your comment where you write an approximate relation for occurence of the roots ,makes me wonder if some sort of approximate $x_n$ can be written if the actual equation is of the form $2\cot(x) = \frac{Kx}{hL} - \frac{hL}{Kx}$ . I wrote the equation in the original question for the parameter values $K=16,L=0.25,h=10.$ – Avrana Mar 16 '19 at 08:56
  • Yes, you can do the following with any $K$, $L$, $h$. Define a series expansion c[x_] = Normal[Series[2 Cot[x], {x, 0, 3}]] (or any desired polynomial order), then a good approximation to the $n$th root (counting from $n=0$) is X[n_] = x /. Solve[c[x - n π] == 32 x/5 - 1563/(10000 x), x, Reals][[3]] (it's a Root object). To get an explicit formula, use Y[n_] = Normal[Series[X[n], {n, ∞, 3}]]. – Roman Mar 16 '19 at 09:09
  • For general $K$, $L$, $h$ this recipe is c[x_] = Normal[Series[2 Cot[x], {x, 0, 1}]] (or higher-order if desired) followed by the approximate root definition X[{k_, L_, h_}, n_] = Assuming[k > 0 && L > 0 && h > 0, x /. Solve[c[x - n π] == (k x)/(h L) - (h L)/(k x), x, Reals][[3]] // Refine]. This gives Y[{k_, L_, h_}, n_] = Normal[Series[X[n], {n,∞, 1}]] the result n π + (2 h L)/(k n π). If you're patient you can get higher-order approximations with this prescription. – Roman Mar 16 '19 at 09:34
  • @Roman Thanks a lot. These were very explanatory. Just downloaded your book on Mathematica for Quantum Physics. Seems really hands-on and well explained. – Avrana Mar 16 '19 at 09:43
  • Enjoy! Let me know if you have any questions about it or find any bugs. – Roman Mar 16 '19 at 09:48
  • @Roman I apologize since this is a very old thread. In one of the comments above where you suggest a general recipie for $K,L,h$, I have been unable to reproduce the final result of n π + (2 h L)/(k n π). I just get back X[n]. Would it be possible for you to have a look at this again ? – Avrana May 24 '20 at 05:45
  • @IndrasisMitra I simply forgot some of the parameters of X. Using Y[{k_, L_, h_}, n_] = Normal[Series[X[{k, L, h}, n], {n, ∞, 1}]] works better. – Roman May 24 '20 at 11:08
  • @Roman I actually already tried putting in the parameters as you suggested in your comment before asking you the question today. But it still keeps the Root object form. I have added a picture at the end of the original question showing it. Am I missing something ? – Avrana May 24 '20 at 11:13
  • @IndrasisMitra what version of Mathematica are you using? $Version – Roman May 24 '20 at 14:35
  • @Roman Mathematica for Windows 11.0.1 – Avrana May 24 '20 at 14:55
  • 1
    That's almost four years old; probably things have changed. – Roman May 24 '20 at 14:59

1 Answers1

3
roots = Sort[x /. 
  NSolve[{2*Cot[x] == Rationalize[6.4] x - Rationalize[0.1563]/x, 60 > x > 0}, x, Reals]];

{0.551848, 3.23803, 6.33252, 9.45782, 12.5912, 15.7278, 18.8661, 22.0053, 25.1452, 28.2854, 31.4259, 34.5666, 37.7074, 40.8484, 43.9894, 47.1305, 50.2717, 53.4129, 56.5542, 59.6955}

Plot[{2*Cot[x], 6.4 x - 0.1563/x}, {x, 0, Last[roots] + 1}, 
 PlotPoints -> 100, MaxRecursion -> 7, 
 Epilog -> {PointSize[Large], Red, Point[{#, 6.4 # - 0.1563/#} & /@ roots]}]

enter image description here

Roman
  • 47,322
  • 2
  • 55
  • 121
kglr
  • 394,356
  • 18
  • 477
  • 896