How to do a fit on multiple peak with a voigt function

Question

I looked a lot on the other questions to do that but I can't find a way to do it properly. So here is my question. I have a spectrum of OH and I would like to do a voigt fit on every peak it has to be able to have the specific intensity of every peak. Lot of other topics are about that but I am not sure I really understand how to do a voigt fit on multiple peak with Mathematica.

Here are my data that I am working with :

    Data = {{307.585, 0.968687}, {307.59, 0.984}, {307.595, 0.993438}, {307.6, 
  0.9895}, {307.605, 1.00175}, {307.61, 0.9995}, {307.615, 
  1.01413}, {307.62, 1.00263}, {307.625, 1.01638}, {307.63, 
  0.997625}, {307.635, 0.9855}, {307.64, 0.999813}, {307.645, 
  0.992}, {307.65, 1.00281}, {307.655, 0.993813}, {307.66, 
  0.992438}, {307.665, 1.00331}, {307.67, 0.994438}, {307.675, 
  1.00512}, {307.68, 0.998563}, {307.685, 1.00006}, {307.69, 
  0.976312}, {307.695, 0.999563}, {307.7, 0.979375}, {307.705, 
  1.00238}, {307.71, 1.08588}, {307.715, 1.32112}, {307.72, 
  1.65425}, {307.725, 1.977}, {307.73, 2.02975}, {307.735, 
  1.799}, {307.74, 1.44969}, {307.745, 1.18444}, {307.75, 
  1.03244}, {307.755, 0.99925}, {307.76, 0.997562}, {307.765, 
  0.982062}, {307.77, 0.983625}, {307.775, 0.982875}, {307.78, 
  1.00312}, {307.785, 1.00256}, {307.79, 0.998875}, {307.795, 
  0.989188}, {307.8, 0.998}, {307.805, 1.01538}, {307.81, 
  0.997}, {307.815, 1.00831}, {307.82, 1.01325}, {307.825, 
  1.03444}, {307.83, 1.054}, {307.835, 1.0545}, {307.84, 
  1.0505}, {307.845, 1.05038}, {307.85, 1.15325}, {307.855, 
  1.59925}, {307.86, 2.407}, {307.865, 3.21856}, {307.87, 
  3.59506}, {307.875, 3.2045}, {307.88, 2.37569}, {307.885, 
  1.63075}, {307.89, 1.17913}, {307.895, 1.04088}, {307.9, 
  1.01594}, {307.905, 1.00413}, {307.91, 1.01469}, {307.915, 
  1.00581}, {307.92, 0.99575}, {307.925, 0.992063}, {307.93, 
  0.994937}, {307.935, 1.00269}, {307.94, 0.989563}, {307.945, 
  0.995563}, {307.95, 0.998438}, {307.955, 0.9895}, {307.96, 
  1.00144}, {307.965, 1.01575}, {307.97, 1.01144}, {307.975, 
  0.99425}, {307.98, 1.01238}, {307.985, 1.01506}, {307.99, 
  1.01719}, {307.995, 1.02338}, {308., 1.17644}, {308.005, 
  1.77269}, {308.01, 2.81981}, {308.015, 3.90187}, {308.02, 
  4.46463}, {308.025, 4.04138}, {308.03, 3.11194}, {308.035, 
  2.25169}, {308.04, 1.88525}, {308.045, 1.83681}, {308.05, 
  1.74675}, {308.055, 1.52794}, {308.06, 1.28481}, {308.065, 
  1.09788}, {308.07, 1.03413}, {308.075, 1.01856}, {308.08, 
  1.02275}, {308.085, 0.989063}, {308.09, 1.01906}, {308.095, 
  0.995}, {308.1, 1.0095}, {308.105, 0.988813}, {308.11, 
  1.00487}, {308.115, 1.00144}, {308.12, 1.00262}, {308.125, 
  0.996625}, {308.13, 1.03056}, {308.135, 1.022}, {308.14, 
  1.03144}, {308.145, 1.03181}, {308.15, 1.03506}, {308.155, 
  1.06725}, {308.16, 1.31431}, {308.165, 2.1235}, {308.17, 
  3.38831}, {308.175, 4.9175}, {308.18, 5.87581}, {308.185, 
  5.74775}, {308.19, 4.83038}, {308.195, 3.42113}, {308.2, 
  2.26788}, {308.205, 1.49631}, {308.21, 1.13788}, {308.215, 
  1.04681}, {308.22, 1.04788}, {308.225, 1.04731}, {308.23, 
  1.03281}, {308.235, 1.04094}, {308.24, 1.01475}, {308.245, 
  1.01363}, {308.25, 1.00431}, {308.255, 1.00613}, {308.26, 
  1.01381}, {308.265, 1.0135}, {308.27, 1.00413}, {308.275, 
  1.02675}, {308.28, 1.01494}, {308.285, 1.01081}, {308.29, 
  1.0085}, {308.295, 1.02787}, {308.3, 1.00119}, {308.305, 
  1.01163}, {308.31, 1.01306}, {308.315, 1.02975}, {308.32, 
  0.9995}, {308.325, 1.02456}, {308.33, 1.0605}, {308.335, 
  1.45588}, {308.34, 2.4695}, {308.345, 3.80994}, {308.35, 
  4.98481}, {308.355, 5.14675}, {308.36, 4.25856}, {308.365, 
  3.03694}, {308.37, 1.89775}, {308.375, 1.34012}, {308.38, 
  1.10706}, {308.385, 1.02663}, {308.39, 1.01888}, {308.395, 
  1.041}, {308.4, 1.00581}, {308.405, 1.00519}, {308.41, 
  1.02006}, {308.415, 1.10962}, {308.42, 1.22213}, {308.425, 
  1.36213}, {308.43, 1.44394}, {308.435, 1.36038}, {308.44, 
  1.22569}, {308.445, 1.09231}, {308.45, 1.01162}, {308.455, 
  1.02156}, {308.46, 1.01494}, {308.465, 1.01706}, {308.47, 
  1.01081}, {308.475, 1.02575}, {308.48, 1.01919}, {308.485, 
  1.04019}, {308.49, 1.03088}, {308.495, 1.0175}, {308.5, 
  1.01838}, {308.505, 1.02694}, {308.51, 1.03119}, {308.515, 
  1.03012}, {308.52, 1.06844}, {308.525, 1.16769}, {308.53, 
  1.81881}, {308.535, 3.02675}, {308.54, 4.33706}, {308.545, 
  5.10806}, {308.55, 4.70069}, {308.555, 3.5655}, {308.56, 
  2.37969}, {308.565, 1.55156}, {308.57, 1.21244}, {308.575, 
  1.08725}, {308.58, 1.04519}, {308.585, 1.03481}, {308.59, 
  1.02656}, {308.595, 1.01956}, {308.6, 1.03494}, {308.605, 
  1.02556}, {308.61, 1.02181}, {308.615, 0.995125}, {308.62, 
  1.006}, {308.625, 1.02188}, {308.63, 1.013}, {308.635, 
  1.014}, {308.64, 1.02613}, {308.645, 1.13438}, {308.65, 
  1.52912}, {308.655, 2.22869}, {308.66, 2.91225}, {308.665, 
  3.17331}, {308.67, 2.79613}, {308.675, 2.11625}, {308.68, 
  1.46975}, {308.685, 1.13725}, {308.69, 1.04094}, {308.695, 
  1.02663}, {308.7, 1.04}, {308.705, 1.02838}, {308.71, 
  1.02319}, {308.715, 1.02244}, {308.72, 1.02863}, {308.725, 
  1.021}, {308.73, 1.03469}, {308.735, 1.05819}, {308.74, 
  1.23556}, {308.745, 1.98969}, {308.75, 3.182}, {308.755, 
  4.37581}, {308.76, 4.79488}, {308.765, 4.14456}, {308.77, 
  3.08075}, {308.775, 2.025}, {308.78, 1.39906}, {308.785, 
  1.18525}, {308.79, 1.08887}, {308.795, 1.02506}, {308.8, 
  1.01706}, {308.805, 1.00869}, {308.81, 1.01669}, {308.815, 
  1.0245}, {308.82, 1.02513}, {308.825, 1.00969}, {308.83, 
  1.0225}, {308.835, 1.005}, {308.84, 1.00925}, {308.845, 
  1.027}, {308.85, 1.01756}, {308.855, 1.01419}, {308.86, 
  1.008}, {308.865, 1.03637}, {308.87, 1.02563}, {308.875, 
  1.02987}, {308.88, 1.03044}, {308.885, 1.03369}, {308.89, 
  1.04175}, {308.895, 1.027}, {308.9, 1.02044}, {308.905, 
  1.04663}, {308.91, 1.02088}, {308.915, 1.01538}, {308.92, 
  1.01469}, {308.925, 1.03613}, {308.93, 1.01825}, {308.935, 
  1.005}, {308.94, 1.03338}, {308.945, 1.02606}, {308.95, 
  1.01888}, {308.955, 1.03213}, {308.96, 1.02881}, {308.965, 
  1.05925}, {308.97, 1.06281}, {308.975, 1.08244}, {308.98, 
  1.30875}, {308.985, 2.11388}, {308.99, 3.51994}, {308.995, 
  5.49638}, {309., 7.35681}, {309.005, 8.16613}, {309.01, 
  7.79706}, {309.015, 6.11356}, {309.02, 4.04888}, {309.025, 
  2.39756}, {309.03, 1.469}, {309.035, 1.22219}, {309.04, 
  1.32281}, {309.045, 1.79588}, {309.05, 2.79619}, {309.055, 
  3.89912}, {309.06, 4.82381}, {309.065, 4.989}, {309.07, 
  4.411}, {309.075, 3.39825}, {309.08, 2.35837}, {309.085, 
  1.66288}, {309.09, 1.28975}, {309.095, 1.10163}, {309.1, 
  1.06494}, {309.105, 1.06863}, {309.11, 1.06031}, {309.115, 
  1.04081}, {309.12, 1.04369}, {309.125, 1.14488}, {309.13, 
  1.62025}, {309.135, 2.47756}, {309.14, 3.47856}, {309.145, 
  4.2975}, {309.15, 4.878}, {309.155, 5.06025}, {309.16, 
  5.01081}, {309.165, 4.32825}, {309.17, 3.28638}, {309.175, 
  2.20669}, {309.18, 1.41925}, {309.185, 1.10706}, {309.19, 
  1.08219}, {309.195, 1.04494}, {309.2, 1.04431}, {309.205, 
  1.02656}, {309.21, 1.0345}, {309.215, 1.03631}, {309.22, 
  1.0375}, {309.225, 1.04394}, {309.23, 1.02106}, {309.235, 
  1.03}, {309.24, 1.04619}, {309.245, 1.12006}, {309.25, 
  1.50838}, {309.255, 2.28694}, {309.26, 3.18419}, {309.265, 
  3.68188}, {309.27, 3.40044}, {309.275, 2.71719}, {309.28, 
  2.03525}, {309.285, 1.69169}, {309.29, 2.09281}, {309.295, 
  2.97788}, {309.3, 3.85825}, {309.305, 4.23231}, {309.31, 
  3.748}, {309.315, 2.749}, {309.32, 1.78506}, {309.325, 
  1.2255}, {309.33, 1.06156}, {309.335, 1.03138}, {309.34, 
  1.03638}, {309.345, 1.03281}, {309.35, 1.03931}, {309.355, 
  1.04756}, {309.36, 1.02138}, {309.365, 1.04319}, {309.37, 
  1.03713}, {309.375, 1.04688}, {309.38, 1.09106}, {309.385, 
  1.30163}, {309.39, 1.59925}, {309.395, 1.8995}, {309.4, 
  1.96169}, {309.405, 1.77063}, {309.41, 1.44662}, {309.415, 
  1.16156}, {309.42, 1.05119}, {309.425, 1.01925}, {309.43, 
  1.00969}, {309.435, 1.02869}, {309.44, 1.005}, {309.445, 
  0.99575}, {309.45, 1.00956}, {309.455, 1.02031}, {309.46, 
  1.09056}, {309.465, 1.15687}, {309.47, 1.39525}, {309.475, 
  1.96163}, {309.48, 2.83544}, {309.485, 3.6045}, {309.49, 
  3.85306}, {309.495, 3.26944}, {309.5, 2.383}, {309.505, 
  1.57263}, {309.51, 1.16694}, {309.515, 1.05038}, {309.52, 
  1.04013}, {309.525, 1.03044}, {309.53, 1.04888}, {309.535, 
  1.01331}, {309.54, 1.05869}, {309.545, 1.26462}, {309.55, 
  1.82844}, {309.555, 2.50463}, {309.56, 3.04944}, {309.565, 
  2.99925}, {309.57, 2.4785}, {309.575, 1.8445}, {309.58, 
  1.37031}, {309.585, 1.13981}, {309.59, 1.0965}, {309.595, 
  1.049}, {309.6, 1.02038}, {309.605, 1.00475}, {309.61, 
  1.04613}, {309.615, 1.02794}, {309.62, 1.0795}, {309.625, 
  1.45475}, {309.63, 2.246}, {309.635, 3.162}, {309.64, 
  3.82688}, {309.645, 3.70163}, {309.65, 3.3005}, {309.655, 
  2.99019}, {309.66, 2.86788}, {309.665, 2.85806}, {309.67, 
  2.49338}, {309.675, 1.95569}, {309.68, 1.45469}, {309.685, 
  1.23044}, {309.69, 1.20294}, {309.695, 1.3705}, {309.7, 
  1.92369}, {309.705, 2.67213}, {309.71, 3.29569}, {309.715, 
  3.33375}, {309.72, 2.73544}, {309.725, 1.97956}, {309.73, 
  1.36694}, {309.735, 1.08031}, {309.74, 1.02888}, {309.745, 
  1.02038}, {309.75, 1.01394}, {309.755, 1.01031}, {309.76, 
  1.01875}, {309.765, 1.008}, {309.77, 0.985188}, {309.775, 
  0.99425}, {309.78, 1.00975}, {309.785, 1.00294}, {309.79, 
  0.994125}, {309.795, 1.01056}, {309.8, 0.991438}, {309.805, 
  1.01262}, {309.81, 1.00725}, {309.815, 1.01181}, {309.82, 
  1.01637}, {309.825, 1.00125}, {309.83, 1.02419}, {309.835, 
  1.00013}, {309.84, 1.00113}, {309.845, 1.01581}, {309.85, 
  0.994188}, {309.855, 0.997375}, {309.86, 1.03138}, {309.865, 
  1.035}, {309.87, 1.08813}, {309.875, 1.3575}, {309.88, 
  1.87894}, {309.885, 2.39213}, {309.89, 2.65194}, {309.895, 
  2.37619}, {309.9, 1.89519}, {309.905, 1.4375}, {309.91, 
  1.16825}, {309.915, 1.08263}, {309.92, 1.06794}, {309.925, 
  1.04331}, {309.93, 1.04037}, {309.935, 1.04675}, {309.94, 
  1.071}, {309.945, 1.07969}, {309.95, 1.1365}, {309.955, 
  1.2945}, {309.96, 1.71725}, {309.965, 2.33175}, {309.97, 
  3.01831}, {309.975, 3.61006}, {309.98, 3.95956}, {309.985, 
  4.07469}, {309.99, 3.84512}, {309.995, 3.20444}, {310., 
  2.40331}, {310.005, 1.66444}, {310.01, 1.21681}, {310.015, 
  1.0625}, {310.02, 1.02787}, {310.025, 1.00875}, {310.03, 
  1.01531}, {310.035, 1.0235}, {310.04, 1.00363}, {310.045, 
  1.01987}, {310.05, 1.00838}, {310.055, 1.011}, {310.06, 
  1.00469}, {310.065, 0.993625}, {310.07, 1.00319}, {310.075, 
  0.987438}, {310.08, 1.00719}, {310.085, 1.04106}, {310.09, 
  1.03025}, {310.095, 1.02538}, {310.1, 1.02456}, {310.105, 
  1.035}, {310.11, 1.03263}, {310.115, 1.023}, {310.12, 
  1.03975}, {310.125, 1.03138}, {310.13, 1.04844}, {310.135, 
  1.08475}, {310.14, 1.46675}, {310.145, 2.26237}, {310.15, 
  3.23106}, {310.155, 3.84794}, {310.16, 3.61375}, {310.165, 
  2.7575}, {310.17, 1.85219}, {310.175, 1.27013}, {310.18, 
  1.084}, {310.185, 1.05194}, {310.19, 1.0295}, {310.195, 
  1.03113}, {310.2, 1.00769}, {310.205, 1.00469}, {310.21, 
  1.00219}, {310.215, 1.00831}, {310.22, 1.04056}, {310.225, 
  1.04681}, {310.23, 1.14163}, {310.235, 1.4555}, {310.24, 
  1.85206}, {310.245, 2.22894}, {310.25, 2.31238}, {310.255, 
  2.28519}, {310.26, 2.36431}, {310.265, 2.506}, {310.27, 
  2.63737}, {310.275, 2.32031}, {310.28, 1.85213}, {310.285, 
  1.38488}, {310.29, 1.12206}, {310.295, 1.0495}, {310.3, 
  1.04188}, {310.305, 1.04263}, {310.31, 1.0355}, {310.315, 
  1.01844}, {310.32, 1.02563}, {310.325, 1.03788}, {310.33, 
  1.0255}, {310.335, 1.01719}, {310.34, 1.05406}, {310.345, 
  1.17819}, {310.35, 1.509}, {310.355, 2.19981}, {310.36, 
  2.99025}, {310.365, 3.476}, {310.37, 3.39581}, {310.375, 
  2.77113}, {310.38, 1.99656}, {310.385, 1.41688}, {310.39, 
  1.107}, {310.395, 1.07163}, {310.4, 1.05625}, {310.405, 
  1.04144}, {310.41, 1.03506}, {310.415, 1.03688}, {310.42, 
  1.02756}, {310.425, 1.02156}, {310.43, 1.01144}, {310.435, 
  1.001}, {310.44, 1.04363}, {310.445, 1.02912}, {310.45, 
  1.03819}, {310.455, 1.0275}, {310.46, 1.02225}, {310.465, 
  1.01431}, {310.47, 1.02719}, {310.475, 1.01581}, {310.48, 
  1.01006}, {310.485, 1.0345}, {310.49, 1.02856}, {310.495, 
  1.03425}, {310.5, 1.02306}, {310.505, 1.00656}, {310.51, 
  1.03619}, {310.515, 1.02756}, {310.52, 1.02869}, {310.525, 
  1.02338}, {310.53, 1.03481}, {310.535, 1.02437}, {310.54, 
  1.02381}, {310.545, 1.00675}, {310.55, 1.02225}, {310.555, 
  1.01725}, {310.56, 1.03381}, {310.565, 1.04475}, {310.57, 
  1.02931}, {310.575, 1.05456}, {310.58, 1.07119}, {310.585, 
  1.122}, {310.59, 1.36988}, {310.595, 1.72888}, {310.6, 
  2.028}, {310.605, 2.11969}, {310.61, 1.86619}, {310.615, 
  1.522}, {310.62, 1.27381}, {310.625, 1.33313}, {310.63, 
  1.65881}, {310.635, 2.00019}, {310.64, 2.17519}, {310.645, 
  2.02919}, {310.65, 1.69513}, {310.655, 1.34388}, {310.66, 
  1.15831}, {310.665, 1.09569}, {310.67, 1.09906}, {310.675, 
  1.34325}, {310.68, 1.99788}, {310.685, 2.877}, {310.69, 
  3.60363}, {310.695, 3.63025}, {310.7, 2.97288}, {310.705, 
  2.09838}, {310.71, 1.433}, {310.715, 1.12606}, {310.72, 
  1.04075}, {310.725, 1.02588}, {310.73, 1.01406}, {310.735, 
  1.00781}, {310.74, 1.00813}, {310.745, 1.02875}, {310.75, 
  1.01512}, {310.755, 1.03488}, {310.76, 1.03481}, {310.765, 
  1.07894}, {310.77, 1.20919}, {310.775, 1.5095}, {310.78, 
  2.12919}, {310.785, 2.88519}, {310.79, 3.4185}, {310.795, 
  3.494}, {310.8, 2.97156}, {310.805, 2.172}, {310.81, 
  1.53613}, {310.815, 1.17781}, {310.82, 1.07944}, {310.825, 
  1.07988}, {310.83, 1.06619}, {310.835, 1.03781}, {310.84, 
  1.04731}, {310.845, 1.0175}, {310.85, 1.01987}, {310.855, 
  1.01556}, {310.86, 1.01056}, {310.865, 1.01906}, {310.87, 
  1.03269}, {310.875, 1.0155}, {310.88, 1.019}, {310.885, 
  1.00987}, {310.89, 1.01031}, {310.895, 1.03613}, {310.9, 
  1.02169}, {310.905, 1.03975}, {310.91, 1.01319}, {310.915, 
  1.04469}, {310.92, 1.02663}, {310.925, 1.01262}, {310.93, 
  1.021}, {310.935, 1.01463}, {310.94, 1.02494}, {310.945, 
  1.05544}, {310.95, 1.09038}, {310.955, 1.11344}, {310.96, 
  1.25906}, {310.965, 1.50406}, {310.97, 1.73356}, {310.975, 
  1.84594}, {310.98, 1.69413}, {310.985, 1.4335}, {310.99, 
  1.21119}, {310.995, 1.06869}, {311., 1.03394}, {311.005, 
  1.04856}, {311.01, 1.03125}, {311.015, 1.05488}, {311.02, 
  1.05625}, {311.025, 1.06081}, {311.03, 1.01894}, {311.035, 
  1.021}, {311.04, 1.04587}, {311.045, 1.05856}, {311.05, 
  1.21462}, {311.055, 1.41919}, {311.06, 1.59406}, {311.065, 
  1.63106}, {311.07, 1.48462}, {311.075, 1.29431}, {311.08, 
  1.12913}, {311.085, 1.04906}, {311.09, 1.04094}, {311.095, 
  1.035}, {311.1, 1.01581}, {311.105, 0.9985}, {311.11, 
  1.02275}, {311.115, 1.00569}, {311.12, 0.983813}, {311.125, 
  1.01775}, {311.13, 1.01813}, {311.135, 1.00138}, {311.14, 
  1.02731}, {311.145, 1.03419}, {311.15, 1.04206}, {311.155, 
  1.05394}, {311.16, 1.03919}, {311.165, 1.06019}, {311.17, 
  1.05575}, {311.175, 1.02587}, {311.18, 1.02581}, {311.185, 1.028}};

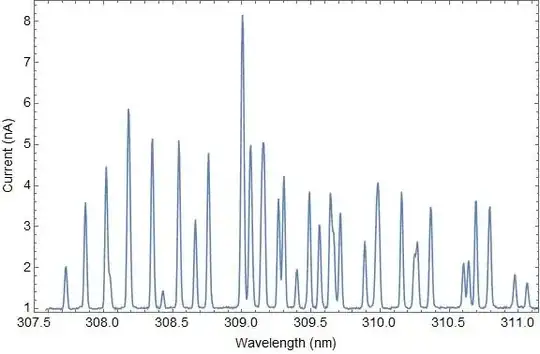
And there is how the peak looks like :

    ListLinePlot[list, PlotRange -> {{307.5, 311.15}, {0.9, 8.5}}, 
 Frame -> True, 
 FrameLabel -> {Text["Wavelength (nm)"], Text["Current (nA)"]}, 
 LabelStyle -> {14, RGBColor[0.`, 0.`, 0.`]}, ImageSize -> Large]

I have tried many ways, like how to perform a multi peak fitting but it is not working with my data and I am a new user of Mathematica.

So thank you a lot for your help,

Francis

Rather than fitting 30 or more voight curves, have you considered using PeakDetect ? — JimB, Mar 20 '19 at 16:02

score 5 · Accepted Answer · answered Mar 20 '19 at 16:12

5

Here's what one can do with PeakDetect:

indices = Select[PeakDetect[data[[All, 2]], 2.5] Range[Length[data[[All, 2]]]], # != 0 &]
Show[ListLinePlot[data, PlotRange -> {{307.5, 311.15}, {0.9, 8.5}}, 
  Frame -> True,
  FrameLabel -> {Text["Wavelength (nm)"], Text["Current (nA)"]},
  LabelStyle -> {14, RGBColor[0.`, 0.`, 0.`]}, ImageSize -> 1000,
  AspectRatio -> 1/8],
 ListPlot[data[[indices, All]], PlotStyle -> {Red, PointSize[0.005]}]]
TableForm[data[[indices, All]], TableHeadings -> {None, {"Wavelength (nm)", "Current(nA)"}}]

answered Mar 20 '19 at 16:12

JimB

41,653
3
48
106

If one has subject matter knowledge that says "values below 1.1 can't be a peak", then adding in the line indices = Select[indices, data[[#, 2]] > 1.1 &] will remove some of the bottom feeders. – JimB Mar 20 '19 at 16:32
Hi, actually I did the same thing with FindPeak, but the problem is that around 310.2 to 310.3 nm, there is two peak that I need to fit with a voigt function to get the exact current of each of them. I can do it with FindPeak but it is not the real value of the maximum current because they are too close from each other. – Francis Labelle Mar 20 '19 at 17:30
1

@FrancisLabelle I doubt that you have sufficient resolution in your data to resolve those peaks reliably. – MarcoB Mar 20 '19 at 19:29
Note that FindPeaks is just a data manipulation method rather than a statistical/probability-based method: There are no measures of precision capable of being estimated. FindPeaks simply does something more consistent (and faster) than what your eye-brain combination can do. If consistency over multiple datasets isn't a requirement, then just let FindPeaks do most of the work and add and/or subtract the peaks that you want added or removed by eye. Just don't expect any measures of precision. – JimB Mar 21 '19 at 03:36
@JimB I was wondering, is it possible to do a gaussian fit on a certain range of data ? For example, I would like to do a gaussian fit for the peak around 308.5 to 308.6 ? This would make it work for what i want to do. Thanks a lot for your answer. – Francis Labelle Apr 23 '19 at 15:03

How to do a fit on multiple peak with a voigt function

1 Answers1