I am trying to solve
My code is
s = NDSolve[{Derivative[3][f][eta] + f[eta] Derivative[2][f][eta] -
Derivative[1][f][eta]^2 + 1 == 0, Derivative[2][theta][eta]
+0.7 f[eta] Derivative[1][theta][eta] = 0, [theta][0] = 1, [theta][#] = 0,
f[0] == 0, f'[0] == -1.18, f'[#] == 0}, f, theta, {eta, 0, 6}] & /@ Range[10, 2, 5];
Plot[Evaluate[f'[eta] /. s], {eta, 0, 6}, PlotRange -> All,
PlotLegends -> (ToString[#] & /@ Range[1, 0, 6])]
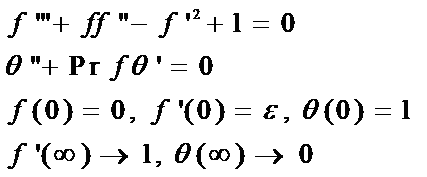

[theta][0] = 1is a syntax error, do you meantheta[0] == 1? – Coolwater Mar 23 '19 at 18:02