6

I am trying to reproduce a network generated by a configuration model given degree vector truncated power law distribution.

I am relying on the following function from the IGraph/M package for Mathematica:

IGDegreeSequenceGame[yy, Method -> "FastSimple"];

where yy is the data and FastSimple is the method option.

An example degree sequence is

yy = {10, 7, 6, 6, 7, 8, 9, 11, 8, 7, 6, 9, 13, 8, 13, 19, 6, 12, 11, 11, 6, 7, 6, 6, 12};

Method doesn't converge; the dimension of yy is 25, and I would like to use it on bigger networks.

Is there a fast way I can generate a network from a configuration model (without loops) with Mathematica?

Szabolcs
  • 234,956
  • 30
  • 623
  • 1,263
Alberto Artoni
  • 61
  • 3
  • Can you give a concrete example for yy? – Szabolcs Mar 26 '19 at 15:14
  • yy is sampled from degree vector truncated power law distribution. An example could be: {10, 7, 6, 6, 7, 8, 9, 11, 8, 7, 6, 9, 13, 8, 13, 19, 6, 12, 11, 11, 6, 7, 6, 6, 12} , where the degree distribution has k0 = 6 as lower cutoff, gamma = 2.5 as power law coefficient, and kmax is the natural cutoff – Alberto Artoni Mar 26 '19 at 15:18
  • 1
    Thanks. Next time please edit all such information into the question itself. I did the edit this time to illustrate what I mean. – Szabolcs Mar 26 '19 at 15:22
  • With FastSimple and the example yy that you provided, I get an immediate output. However, FastSimple does not implement the configuration model, and does not sample uniformly. Did you mean ConfigurationModelSimple? Was it not clear from the documentation that FastSimple is not the configuration model? I welcome all suggestion to improve the documentation. – Szabolcs Mar 26 '19 at 15:25
  • Also, make sure you are using the latest version of IGraph/M (currently 0.3.108) – Szabolcs Mar 26 '19 at 15:29
  • The final intention is to use configuration model. Since it is costly i was trying to change methodto see if I could obtain anyway the results I am looking for. Enlarging yy becomes costly also with FastSimple. – Alberto Artoni Mar 26 '19 at 15:30
  • Try with: [size is 100]

    {9, 69, 24, 16, 9, 6, 40, 33, 7, 18, 6, 7, 7, 35, 7, 15, 10, 6, 23, 11, 16, 25, 20, 13, 16, 77, 8, 10, 8, 11, 9, 10, 10, 9, 27, 8, 77, 33, 7, 7, 15, 10, 7, 6, 17, 13, 6, 63, 7, 7, 6, 7, 8, 15, 11, 6, 6, 8, 7, 7, 9, 6, 6, 6, 6, 8, 36, 6, 10, 8, 10, 8, 6, 6, 8, 14, 8, 6, 12, 6, 11, 10, 6, 6, 50, 8, 17, 6, 8, 16, 12, 10, 9, 8, 7, 7, 13, 12, 8, 6}

     – Alberto Artoni Mar 26 '19 at 15:33
  • This is my sampler: data = RandomVariate[ TruncatedDistribution[{k0, kmax}, ParetoDistribution[k0, [Gamma] - 1]], nodes]; where gamma is the exponent of the power law, k0 the minimal cutoff, kmax is the natural. Currently I am testing with gamma = 2.5, k0 = 6, kmax = nodes-1 – Alberto Artoni Mar 26 '19 at 15:36

1 Answers1

7

Exact sampling with a given degree sequence

The example degree sequence that you provided is:

yy = {10, 7, 6, 6, 7, 8, 9, 11, 8, 7, 6, 9, 13, 8, 13, 19, 6, 12, 11, 11, 6, 7, 6, 6, 12};

With this degree sequence, 

IGDegreeSequenceGame[yy, Method -> "FastSimple"]

returns immediately, contrary to your claim.

However, Method -> "FastSimple" does not implement the configuration model. It implements a similar algorithm that is much faster but does not sample graphs uniformly. In other words, not all graphs that have this degree sequence will be generated with the same probability.

To use the configuration model to generate simple graphs, use 

IGDegreeSequenceGame[yy, Method -> "ConfigurationModelSimple"]

As you say, this will not return. It takes too long. This algorithm (i.e. the configuration model) is simply too slow on this degree sequence, whether implemented in IGraph/M or another package.

I am not aware of any method which is capable of the exact and uniform sampling of simple graphs with such a degree sequence (if you are, let me know).

Approximate sampling with MCMC

One alternative option you have is to use Markov-Chain based sampling. First, create a single realization of the degree sequence then "shuffle its edges around" while keeping the degree sequence with IGRewire. Provided that enough rewiring steps are made, this method will sample approximately uniformly. It would sample uniformly for an infinite number of rewiring steps.

g = IGRealizeDegreeSequence[yy]
IGRewire[g, 1000]

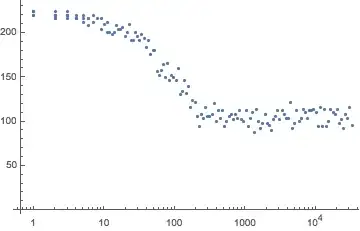
You can use some heuristics to decide on how many rewiring steps are sufficient for the degree sequence you are working with. For example, correlations seem to be lost with less than 1000 rewiring steps for the sequence you quoted.

am = AdjacencyMatrix[g];
ListLogLinearPlot@Table[
  {k, Flatten[am].Flatten@AdjacencyMatrix@IGRewire[g, k]},
  {k, Round[2^Range[0, 15, 0.1]]}
  ]

enter image description here

You can also use Method -> "VigerLatapy" in IGDegreeSequenceGame, which implements a similar method for sampling connected graphs specifically. See the documentation for a reference to the paper.

Sampling graphs with power-law degree distributions

If your goal is to generate a graph with a power-law degree distribution (not a specific degree sequence), also take a look at IGStaticPowerLawGame. See the references within the C/igraph documentation for how it works. It implements a variation of the Chung-Lu model.

A note about the built-in DegreeGraphDistribution

A note about RandomGraph[DegreeGraphDistribution[...]]: it does not sample uniformly and I was not able to get information from Wolfram Support about how this method works. I would be cautious when using it.

Szabolcs
  • 234,956
  • 30
  • 623
  • 1,263
  • Great answer! I was wondering, for a given graph, i) is it possible to rewire such that a topological property such as the clustering increases? If I may ask a 2nd question, but admittedly a tad off topic: ii) if we simply want a graph with a constant degree dist, e.g all degrees set to 4, this would mimic a lattice/ordered graph, would it be equivalent to simply creating a regular graph using RandomGraph[WattsStrogatzGraphDistribution[n,0,2]]? –  Aug 02 '19 at 12:32
  • @user929304 i) I guess it would, but I do not think that you would find an existing implementation. Ideally, this would be implemented in a low-level language (like C) by yourself. E.g. keep doing degree-preserving edge swaps, and accept a swap with higher probability if the clustering increases. ii) No, because the rewiring used in the Watts-Strogatz procedure does not preserve the degrees. BTW: all degrees are the same = this is called a regular graph – Szabolcs Aug 02 '19 at 17:09