Having trouble solving a particular differential equation

Question

I have the following equation:

$$\frac{f(x)}{f'(x)}\left(f(x) + \frac{1+(f'(x))^2}{f''(x)}\right) = c$$

where $c$ is a constant $> 0$.

Mathematica handles this well and I'm able to plot it just fine using NDSolve, but only when $c = 0$. For any other value of $c$, I get errors and the plot comes out all wrong.

Can anyone help me here?

Edit

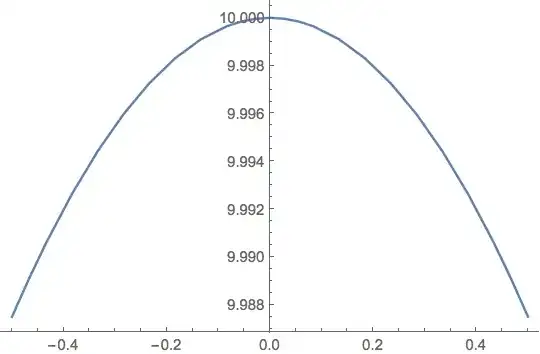
An example of the code I used for NDSolve was:

s = 
  NDSolve[
   {y[x]/y'[x] * (y[x] + (1+(y'[x])^2)/y''[x]) == 1, y[0] == 10, y'[0] == 0}, 
   y, {x, -0.5, 0.5}]

Can you give the NDSolve[] code you used so people don't have to retype things for you? — J. M.'s missing motivation, Mar 31 '19 at 01:44
I don't have any trouble evaluating your example expression. I running V11.3 on macOS 10.13.4. I suggest you try relaunching Mathematica and try with a fresh notebook. — m_goldberg, Mar 31 '19 at 02:07

score 2 · Accepted Answer · answered Mar 31 '19 at 02:17

It sounds to me that the problem might be with plotting, which is discussed in Easy way to plot ODE solutions from NDSolve? The following works without messages.

ListLinePlot@
 NDSolveValue[{y[x]/y'[x]*(y[x] + (1 + (y'[x])^2)/y''[x]) == 1, 
   y[0] == 10, y'[0] == 0}, y, {x, -0.5, 0.5}]

Having trouble solving a particular differential equation

Edit

1 Answers1