I found here a solution by s0rce on how one can for example create a 3d FaceCenteredCubic lattice structure:
basis = LatticeData["FaceCenteredCubic", "Basis"];
points = Tuples[Range[-4, 4], 3].basis;
inside = Select[points, Norm[#] <= 4 &];
Graphics3D[Sphere[inside, 0.25]]
How can I build up a 2d lattice of HexagonalLattice structure and a 3d lattice of HexagonalClosePacking by using LatticeData and find the corresponding coordinates?
I tried the following:
1.
LatticeData[]
{"BaseCenteredMonoclinic", "BaseCenteredOrthorhombic", \
"BodyCenteredCubic", "BodyCenteredOrthorhombic", \
"CenteredTetragonal", "CoxeterTodd", "FaceCenteredCubic", \
"FaceCenteredOrthorhombic", "HexagonalClosePacking", \
"HexagonalLattice", "KorkineZolotarev", "Leech", "SimpleCubic", \
"SimpleHexagonal", "SimpleMonoclinic", "SimpleOrthorhombic", \
"SimpleTetragonal", "SimpleTriclinic", "SimpleTrigonal", \
"SquareLattice", "TetrahedralPacking"}
LatticeData["HexagonalClosePacking", "Properties"]
{"AlternateNames", "AutomorphismGroupOrder", "Basis", \
"CenterDensity", "Classes", "CoveringRadius", "CoxeterNumber", \
"Density", "Determinant", "Dimension", "Dual", "Even", "Extremal", \
"GeneratorMatrix", "Genus", "GlueVectors", "GramMatrix", \
"HermiteInvariant", "Image", "Integral", "KissingNumber", \
"MinimalNorm", "MinimalVectors", "ModularNumber", "Name", \
"Nonextremal", "Nonintegral", "Nonunimodular", "Notation", "Odd", \
"PackingRadius", "QuadraticForm", "RadialFunction", "StandardName", \
"ThetaSeriesFunction", "Thickness", "Unimodular", "Volume"}
LatticeData["HexagonalClosePacking", "Basis"]
Missing["NotApplicable"]
Here I probably need the MinimalVectors to produce the crystal structure, but how?
2.
LatticeData["HexagonalLattice", "Basis"]
SparseArray[Automatic, {2, 2}, 0, {
1, {{0, 2, 3}, {{2}, {1}, {2}}}, {1, -1, -1}}]
How can I get the coordinates from the SparseArray?
Summary:
1.
list1 = LatticeData["HexagonalClosePacking", "Properties"]
Grid[{#, LatticeData["HexagonalClosePacking", #]} & /@ list1,
Frame -> All, Alignment -> Left]
2.
list2 = LatticeData["HexagonalClosePacking", "Properties"]
Grid[{#, LatticeData["HexagonalClosePacking", #]} & /@ list2,
Frame -> All, Alignment -> Left]
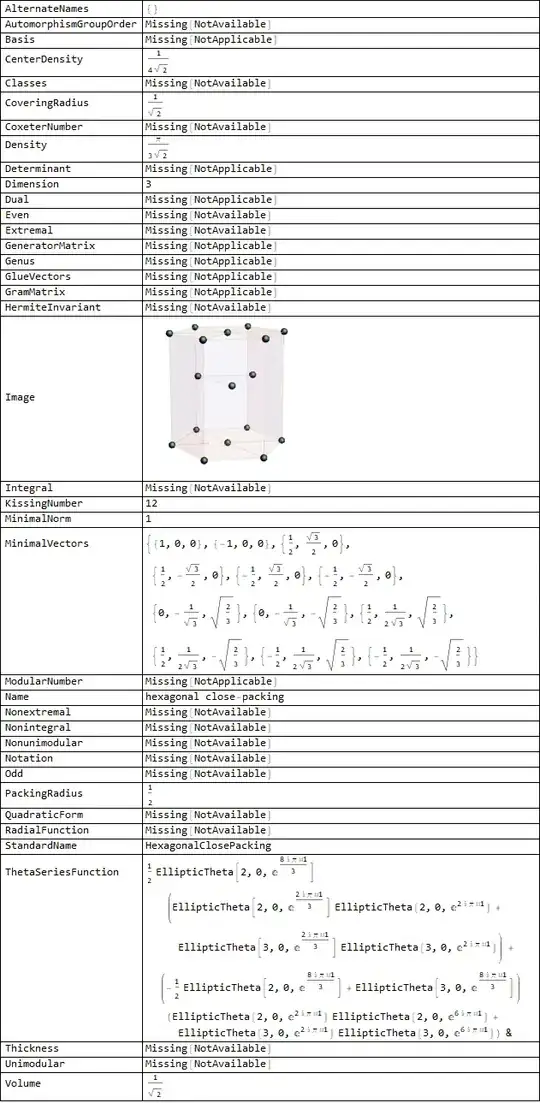
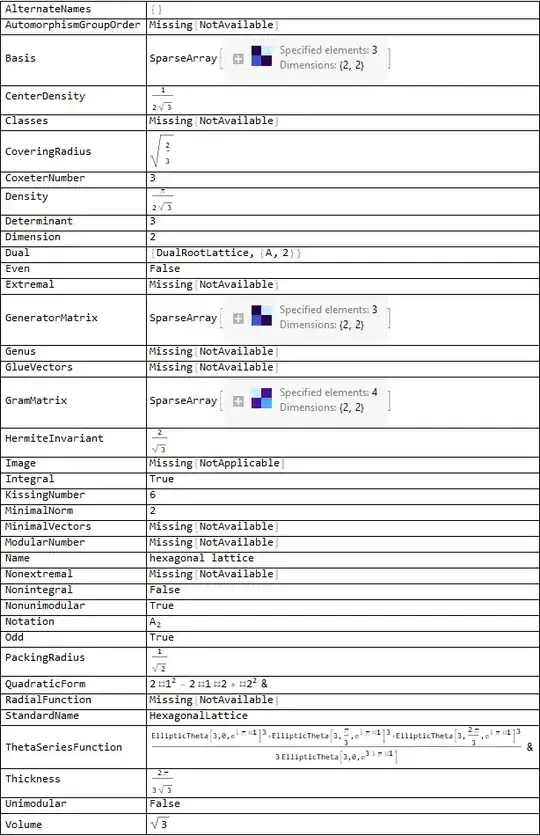
LatticeData. – lio Apr 01 '19 at 15:29LatticeData[]. Why did you fail to get good results? – Somos Apr 01 '19 at 22:21