How can I delete all similar Feynman diagrams in Mathematica?

Question

Ext1 = {0, 0}
Ext2 = {8, 0}
Vc1 = {2, 2}
Vc2 = {5, 2}
I1 = Table[i, {i, 1, 3}]
I2 = Table[i - 1, {i, 2, 7}]
Tuples[I1, 2]
int1 = Select[Tuples[I1, 2],
  Last[#] == 3 && First[#] != 2 || Last[#] == 1 && First[#] == 2 &]
Tuples[I2, 2]
int2 = Select[Tuples[I2, 2],
  Last[#] == 3 && First[#] != 5 && First[#] != 1 && First[#] != 2 && First[#] != 3
  || Last[#] == 1 && First[#] == 5 &]
Do[Graphics[{Black, Thick,
    {Line[{Ext1, int1[[i]]}], Line[{Vc1, int1[[1]]}], 
     Line[{Vc1, int1[[2]]}], Line[{Vc1, int1[[3]]}], 
     Line[{Vc2, int2[[1]]}], Line[{Vc2, int2[[2]]}], 
     Line[{Vc2, int2[[3]]}], Line[{Ext2, int2[[j]]}],
     If[i == 1, {If[j == 1, {Line[{int1[[i + 1]], int2[[j + 1]]}], 
                             Line[{int1[[i + 2]], int2[[j + 2]]}]}],
                 If[j == 2, {Line[{int1[[i + 1]], int2[[j + 1]]}], 
                             Line[{int1[[i + 2]], int2[[j - 1]]}]}],
                 If[j == 3, {Line[{int1[[i + 1]], int2[[j - 1]]}], 
                             Line[{int1[[i + 2]], int2[[j - 2]]}]}]}],
     If[i == 2, {If[j == 1, {Line[{int1[[i + 1]], int2[[j + 1]]}], 
                             Line[{int1[[i - 1]], int2[[j + 2]]}]}],
                 If[j == 2, {Line[{int1[[i + 1]], int2[[j + 1]]}], 
                             Line[{int1[[i - 1]], int2[[j - 1]]}]}],
                 If[j == 3, {Line[{int1[[i + 1]], int2[[j - 1]]}], 
                             Line[{int1[[i - 1]], int2[[j - 2]]}]}]}],
     If[i == 3, {If[j == 1, {Line[{int1[[i - 1]], int2[[j + 1]]}], 
                             Line[{int1[[i - 2]], int2[[j + 2]]}]}],
                 If[j == 2, {Line[{int1[[i - 1]], int2[[j + 1]]}], 
                             Line[{int1[[i - 2]], int2[[j - 1]]}]}],
                 If[j == 3, {Line[{int1[[i - 1]], int2[[j - 1]]}], 
                             Line[{int1[[i - 2]], int2[[j - 2]]}]}]}]
   }}]
   Graphics[{Black, Thick,
    {Line[{Ext1, int1[[i]]}], Line[{Vc1, int1[[1]]}], 
     Line[{Vc1, int1[[2]]}], Line[{Vc1, int1[[3]]}], 
     Line[{Vc2, int2[[1]]}], Line[{Vc2, int2[[2]]}], 
     Line[{Vc2, int2[[3]]}], Line[{Ext2, int2[[j]]}],
     If[i == 1, {If[j == 1, {Line[{int1[[i + 1]], int2[[j + 2]]}], 
                             Line[{int1[[i + 2]], int2[[j + 1]]}]}],
                 If[j == 2, {Line[{int1[[i + 1]], int2[[j - 1]]}], 
                             Line[{int1[[i + 2]], int2[[j + 1]]}]}],
                 If[j == 3, {Line[{int1[[i + 1]], int2[[j - 2]]}], 
                             Line[{int1[[i + 2]], int2[[j - 1]]}]}]}],
     If[i == 2, {If[j == 1, {Line[{int1[[i + 1]], int2[[j + 2]]}], 
                             Line[{int1[[i - 1]], int2[[j + 1]]}]}],
                 If[j == 2, {Line[{int1[[i + 1]], int2[[j - 1]]}], 
                             Line[{int1[[i - 1]], int2[[j + 1]]}]}],
                 If[j == 3, {Line[{int1[[i + 1]], int2[[j - 2]]}], 
                             Line[{int1[[i - 1]], int2[[j - 1]]}]}]}],
     If[i == 3, {If[j == 1, {Line[{int1[[i - 1]], int2[[j + 2]]}], 
                             Line[{int1[[i - 2]], int2[[j + 1]]}]}],
                 If[j == 2, {Line[{int1[[i - 1]], int2[[j - 1]]}], 
                             Line[{int1[[i - 2]], int2[[j + 1]]}]}],
                 If[j == 3, {Line[{int1[[i - 1]], int2[[j - 2]]}], 
                             Line[{int1[[i - 2]], int2[[j - 1]]}]}]}]
   }}] // Print,
  {i, 1, 3}, {j, 1, 3}]

I have attached the diagram though it's not good looking. need help

It is impossible to answer this question when give not code and no description on how want the diagrams to look. — m_goldberg, Apr 09 '19 at 05:50
I have updated all the relevant things now. I want figure like last pic — , Apr 09 '19 at 06:41
Please do not post images of your work, especially when the images display at a size that make them difficult to read. Please post your actual Mathematica code in the form of text that can be copied and pasted into a Mathematica notebook. Without such, it will be difficult to reproduce your problem and to experiment with possible solutions. — m_goldberg, Apr 09 '19 at 06:50
Sorry for inconveniences. Actually, I tried to upload the code but it is so long that it's not uploading. as a new user I 'm not able to make it properly — , Apr 09 '19 at 07:13
Can the downvoteres please calm down a bit! Laboni is a new contributor and needs time to find her way around here. — user21, Apr 09 '19 at 08:44
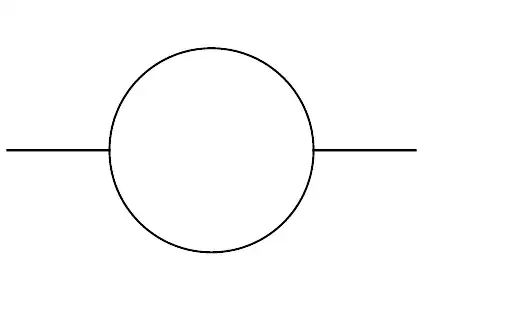
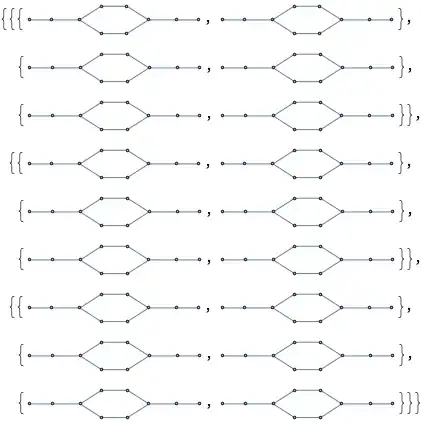
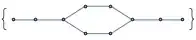
Try to represent each diagram as a Graph. Once you have this format, it's easy to tell which graphs are isomorphic with IsomorphicGraphQ. After that, maybe the plotting functions for graphs are already good enough for your purposes? — Roman, Apr 09 '19 at 09:37
It's difficult to know what you mean by "similar" diagrams. Can you give a specific example? — Carl Lange, Apr 09 '19 at 09:44
Have you seen this? https://mathematica.stackexchange.com/q/170268 — Roman, Apr 09 '19 at 12:04

Roman · Accepted Answer · 2019-04-09T11:57:58.347

Make a list of diagrams by using Table instead of Do with Print:

A = Table[{{Line[{Ext1, int1[[i]]}], Line[{Vc1, int1[[1]]}], 
            Line[{Vc1, int1[[2]]}], Line[{Vc1, int1[[3]]}], 
            Line[{Vc2, int2[[1]]}], Line[{Vc2, int2[[2]]}], 
            Line[{Vc2, int2[[3]]}], Line[{Ext2, int2[[j]]}], 
      If[i == 1, {If[j == 1, {Line[{int1[[i + 1]], int2[[j + 1]]}], 
                              Line[{int1[[i + 2]], int2[[j + 2]]}]}], 
                  If[j == 2, {Line[{int1[[i + 1]], int2[[j + 1]]}], 
                              Line[{int1[[i + 2]], int2[[j - 1]]}]}], 
                  If[j == 3, {Line[{int1[[i + 1]], int2[[j - 1]]}], 
                              Line[{int1[[i + 2]], int2[[j - 2]]}]}]}], 
      If[i == 2, {If[j == 1, {Line[{int1[[i + 1]], int2[[j + 1]]}], 
                              Line[{int1[[i - 1]], int2[[j + 2]]}]}], 
                  If[j == 2, {Line[{int1[[i + 1]], int2[[j + 1]]}], 
                              Line[{int1[[i - 1]], int2[[j - 1]]}]}], 
                  If[j == 3, {Line[{int1[[i + 1]], int2[[j - 1]]}], 
                              Line[{int1[[i - 1]], int2[[j - 2]]}]}]}], 
      If[i == 3, {If[j == 1, {Line[{int1[[i - 1]], int2[[j + 1]]}], 
                              Line[{int1[[i - 2]], int2[[j + 2]]}]}], 
                  If[j == 2, {Line[{int1[[i - 1]], int2[[j + 1]]}], 
                              Line[{int1[[i - 2]], int2[[j - 1]]}]}], 
                  If[j == 3, {Line[{int1[[i - 1]], int2[[j - 1]]}], 
                              Line[{int1[[i - 2]], int2[[j - 2]]}]}]}]},
           {Line[{Ext1, int1[[i]]}], Line[{Vc1, int1[[1]]}],
            Line[{Vc1, int1[[2]]}], Line[{Vc1, int1[[3]]}],
            Line[{Vc2, int2[[1]]}], Line[{Vc2, int2[[2]]}],
            Line[{Vc2, int2[[3]]}], Line[{Ext2, int2[[j]]}], 
      If[i == 1, {If[j == 1, {Line[{int1[[i + 1]], int2[[j + 2]]}], 
                              Line[{int1[[i + 2]], int2[[j + 1]]}]}], 
                  If[j == 2, {Line[{int1[[i + 1]], int2[[j - 1]]}], 
                              Line[{int1[[i + 2]], int2[[j + 1]]}]}], 
                  If[j == 3, {Line[{int1[[i + 1]], int2[[j - 2]]}], 
                              Line[{int1[[i + 2]], int2[[j - 1]]}]}]}], 
      If[i == 2, {If[j == 1, {Line[{int1[[i + 1]], int2[[j + 2]]}], 
                              Line[{int1[[i - 1]], int2[[j + 1]]}]}], 
                  If[j == 2, {Line[{int1[[i + 1]], int2[[j - 1]]}], 
                              Line[{int1[[i - 1]], int2[[j + 1]]}]}], 
                  If[j == 3, {Line[{int1[[i + 1]], int2[[j - 2]]}], 
                              Line[{int1[[i - 1]], int2[[j - 1]]}]}]}], 
      If[i == 3, {If[j == 1, {Line[{int1[[i - 1]], int2[[j + 2]]}], 
                              Line[{int1[[i - 2]], int2[[j + 1]]}]}], 
                  If[j == 2, {Line[{int1[[i - 1]], int2[[j - 1]]}], 
                              Line[{int1[[i - 2]], int2[[j + 1]]}]}], 
                  If[j == 3, {Line[{int1[[i - 1]], int2[[j - 2]]}], 
                              Line[{int1[[i - 2]], int2[[j - 1]]}]}]}]}},
  {i, 1, 3}, {j, 1, 3}]

The plots from the original post can be recovered from this with

Map[Graphics, A, {3}]

Convert a line assembly to a graph: (thanks to @Szabolcs)

tograph[X_] := 
  CanonicalGraph[DeleteCases[Flatten[X], Null] /.
    Line[{a_, b_}] -> (a \[UndirectedEdge] b)]

Convert all diagrams to graphs:

B = Map[tograph, A, {3}]

It looks like they are all isomorphic and thus all diagrams are the same:

DeleteDuplicates[Flatten[B]]

In case your graph edges are directional, you can use

todirectedgraph[X_] :=
  CanonicalGraph[DeleteCases[Flatten[X], Null] /. 
    Line[{a_, b_}] -> (a \[DirectedEdge] b)]

which gives directed graphs. They also all turn out to be isomorphic to each other:

B = Map[todirectedgraph, A, {3}];
DeleteDuplicates[Flatten[B]]

The efficient way to eliminate isomorphic duplicates is DeleteDuplicatesBy[list, CanonicalGraph]. This avoids doing all pairwise checks. — Szabolcs, Apr 09 '19 at 10:44
There is one issue though: a Feynman diagram can in general be a multigraph, which is not supported by IsomorphicGraphQ or CanonicalGraph. IGraph/M has IGIsomorphicQ, which does support multigraphs. It also has IGBlissCanonicalGraph, which does not. However, it does support vertex-coloured graphs, which in principle can be used to implement multigraph support. — Szabolcs, Apr 09 '19 at 10:46
More generally, a Feynman diagram is an edge-coloured multigraph, which makes things even more complicated, but I think that once we have support for *basic( coloured graphs (IGraph/M does) it can be used to implement full support for the more complicated cases. — Szabolcs, Apr 09 '19 at 10:47
Thanks for the comments, @Szabolcs. I've added the CanonicalGraph function to the tograph facility, so that the resulting graphs can be compared directly with DeleteDuplicates. Going into details of what Feynman diagrams are and how to represent them: I agree that it's more complex than what @Laboni presents; here I'm merely reacting to her code. — Roman, Apr 09 '19 at 10:55

How can I delete all similar Feynman diagrams in Mathematica?

1 Answers1