Plotting an osculating circle at the leading edge of a developing Cornu spiral

Question

I need to plot an interactive Cornu spiral like so:

Manipulate[
  ParametricPlot[{FresnelC[M*t], FresnelS[M*t]}, {t, 0, 1}, 
    PlotRange -> {{0, 1}, {0, 1}}], {M, 0, 3}]

But I also want to add an osculating circle to the plot at the leading point of the developing spiral so that, as the spiral develops, the circle illustrates the radius of curvature at the leading point.

I've tried several different methods of generating the circle, but none of them have worked for me. Any help would be appreciated.

Can you show us what you’ve tried so far? Maybe we can help you fix it. — MarcoB, Apr 11 '19 at 01:06
As b3m2a1 notes 167096 is related and is exactly what i had tried but i couldn't figure out how to adapt the function used in that example to the cornu spiral — TheFarstrider, Apr 11 '19 at 16:30

score 6 · Accepted Answer · edited Jun 16 '20 at 09:23

I used formulae from this MathWorld article to find the center of curvature. Having this point, it is easy to draw the radius of curvature. I modified your Manipulate expression to do that. Here is the code.

Functions for computing points on the spiral and and the 1st and 2nd derivatives component-wise.

cornu[u_] := {FresnelC[u ], FresnelS[u]}
d1FC[u_] = D[FresnelC[u ], u];
d1FS[u_] = D[FresnelS[u ], u];
d2FC[u_] = D[FresnelC[u ], {u, 2}];
d2FS[u_] = D[FresnelS[u ], {u, 2}]

cornuCC[u] computes the center of curvature of the spiral at point cornu[u].

conuCC[u_] :=
  Module[{x0, y0, w},
    {x0, y0} = cornu[u];
    w = (d1FC[u]^2 + d1FS[u]^2)/(d1FC[u] d2FS[u] - d2FC[u] d1FS[u]);
    {x0 - w d1FS[u], y0 + w d1FC[u]}]
Manipulate[
  ParametricPlot[cornu[m t], {t, 0, 1},
    Epilog ->
      {Red, AbsolutePointSize[8], 
       Point[{cornu[m], conuCC[m]}], Line[{cornu[m], conuCC[m]}]},
     PlotRange -> {{0, 1}, {0, 1}}],
  {m, .1, 3, .05, Appearance -> {Large, "Labeled"}}]

I think showing the radius of curvature as a line along with the center of curvature and the leading tip of the spiral as points gives the observer a better feel for the curvature than an osculating circle would. If you disagree, I leave it as an exercise for you to make the change, which is easy.

Update

This update addresses an issue raised by the OP in a comment below.

Adding an annotation that tracks the value of the radius of curvature is not hard. However, adding it to what is already being tracked makes it a good idea to refactor the code so the pair {cornu[m], conuCC[m]}, which gives the endpoints of radius of curvature, is computed only once in each update of the Manipulate expression. This is done like so:

  Manipulate[
    pts = {cornu[m], conuCC[m]};
    ParametricPlot[cornu[m t], {t, 0, 1},
      Epilog -> {Red, AbsolutePointSize[8], Point[pts], Line[pts]},
      PlotRange -> {{0, 1}, {0, 1}}],
    {pts, None},
    {m, .1, 3, .05, Appearance -> {Large, "Labeled"}},
    Dynamic @ Style[Row[{"Radius of curvature: ", ArcLength[Line[pts]]}], 12]]

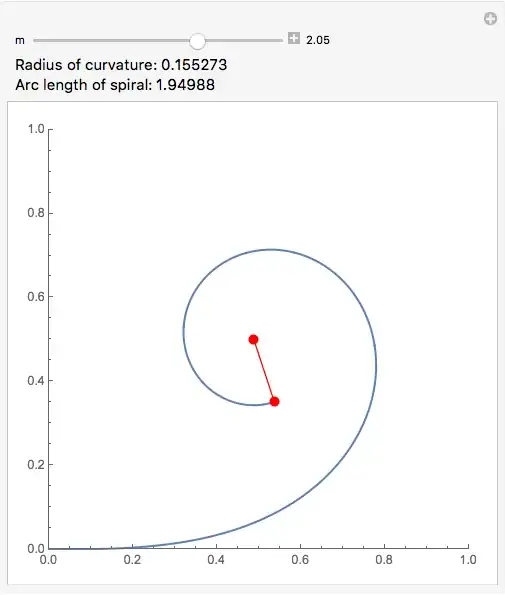
Update2

It seems the OP wants the arc length of the spiral displayed, too. OK, I'll add that.

cornuPts[m_] := Table[cornu[i], {i, 0, m, .01}]
Manipulate[
  pts = {cornu[m], conuCC[m]};
  ParametricPlot[cornu[m t], {t, 0, 1}, 
    Epilog -> {Red, AbsolutePointSize[8], Point[pts], Line[pts]}, 
    PlotRange -> {{0, 1}, {0, 1}}], {pts, None}, {m, .1, 3, .05, 
    Appearance -> {Large, "Labeled"}}, 
  Dynamic @ Style[Row[{"Radius of curvature: ", ArcLength[Line[pts]]}], 12],
  Dynamic @ Style[Row[{"Arc length of spiral: ", ArcLength[Line[cornuPts[m]]]}], 12]]

This is almost entirely what im looking for. The only addition i need to this is to add something to the Manipulate that displays the length of the Red segment. — TheFarstrider, Apr 11 '19 at 16:18
@TheFarstrider. It would seem you want more than you asked for above. I have added tracking arc length. — m_goldberg, Apr 11 '19 at 23:20
Im sorry for expanding the parameters of the question. It came up upon discussion of the result with my colleagues. Thank you for your help. — TheFarstrider, Apr 12 '19 at 03:06

score 1 · Answer 2 · answered Nov 13 '19 at 22:29

The code in the answer b3m2a1 linked to was intended for 3D curves, which is why it had a lot of machinery embedded. For plane curves, things are vastly simpler:

osculatingCircle[fun_?VectorQ, {t_, tvalue_}] := Module[{ka, nv, tv},
    {{ka}, {tv, nv}} = FrenetSerretSystem[fun, t] /. t -> tvalue;
    Circle[(fun /. t -> tvalue) + nv/ka, 1/Abs[ka]]]

Thus, here is a Manipulate[] for the clothoid:

Manipulate[With[{oc = osculatingCircle[cornu[t], {t, m}]}, 
                ParametricPlot[cornu[m t], {t, 0, 1}, 
                               Epilog -> {Directive[Red, AbsolutePointSize[8]], 
                                          Through[{Line, Point}[{cornu[m], First[oc]}]]}, 
                               PlotLabel -> StringForm["Radius of curvature: `1`\n Arc length of spiral: `2`",
                                                       Round[Last[oc], 1.*^-6],
                                                       Round[m, 1.*^-6]], 
                               PlotRange -> {{0, 1}, {0, 1}}, Prolog -> {Gray, oc}]],
           {m, .1, 3, .05, Appearance -> {Large, "Labeled"}}, 
           Initialization :> (cornu[t_] := {FresnelC[t], FresnelS[t]}), 
           SaveDefinitions -> True]

Manipulate

Plotting an osculating circle at the leading edge of a developing Cornu spiral

2 Answers2

Update

Update2