I have some data :
data={{9., 16.8895}, {12., 17.3404}, {15., 17.1633}, {18., 19.3417}, {21., 17.9899}, {24., 19.9677}, {27., 19.4362}, {30., 20.6519}, {33., 19.4591}, {36., 20.6855}, {39., 20.1952}, {42., 21.9949}, {45., 21.0234}, {48., 22.7408}, {51., 22.3908}, {54., 25.0918}, {57., 23.5989}, {60., 26.0703}, {63., 24.5605}, {66., 27.2539}, {69.,
26.1619}, {72., 28.4762}, {75., 27.5854}, {78., 29.8393}, {81., 28.3553}, {84., 30.3221}, {87., 29.675}, {90., 31.5653}, {93., 30.5337}, {96., 33.3734}, {99., 31.6876}, {102., 34.1503}, {105., 33.3065}, {108., 35.3291}, {111., 33.9209}, {114., 36.773}, {117., 35.4094}, {120., 41.5902}, {123., 36.1305}, {126., 37.971}, {129.,
36.402}, {132., 39.1158}, {135., 38.0177}, {138., 40.8558}, {141.,
39.6065}, {144., 40.9749}, {147., 39.8896}, {150., 41.8237}, {153.,
40.5802}, {156., 42.3858}, {159., 40.6619}, {162., 44.4442}, {165.,
45.4162}, {168., 46.1884}, {171., 44.6008}, {174., 47.1647}, {177.,
45.3808}, {180., 46.5859}, {183., 45.3035}, {186., 47.6604}, {189.,
46.6771}, {192., 45.9242}, {195., 46.767}, {198., 44.6899}, {201.,
46.6628}, {204., 46.1571}, {207., 46.5555}, {210., 44.835}, {213.,
45.1423}, {216., 45.1954}, {219., 45.309}, {222., 47.7791}, {225.,
46.7777}, {228., 48.135}, {231., 45.6493}, {234., 45.8933}, {237.,
46.1803}, {240., 46.7285}, {243., 46.8063}, {246., 47.1679}, {249.,
46.8787}, {252., 47.2715}, {255., 47.5362}, {258., 48.9234}, {261.,
47.5456}, {264., 53.5554}, {267., 52.5704}, {270., 49.6049}, {273.,
49.1189}, {276., 48.9498}, {279., 49.6024}, {282., 49.7491}, {285.,
53.1681}, {288., 51.7124}, {291., 50.8069}, {294., 50.0237}, {297.,
50.5922}, {300., 50.6518}}
That I would like to fit :
model[a_?NumberQ, R0_?NumberQ, c_?NumberQ, d_?NumberQ, Rc_?NumberQ] :=
Module[{y, m, x}, First[y /. NDSolve[{y'[
x] == (0.18*(1 - a*m[x]/(1 + m[x])) -
0.00462* (y[x] - R0))*(UnitStep[Rc - R0]) + (1 -
UnitStep[Rc - R0])*0.18,
m'[x] == UnitStep[Rc - R0]*(c*(y[x]^3 - R0^3) - d*m[x]),
y[0] == R0, m[0] == 0}, {y, m}, {x, 0, 310}]]]
nlm = NonlinearModelFit[data, model[a, 12, c, d, Rc][x], {a, c, d, Rc}, x, Method -> "Gradient"]
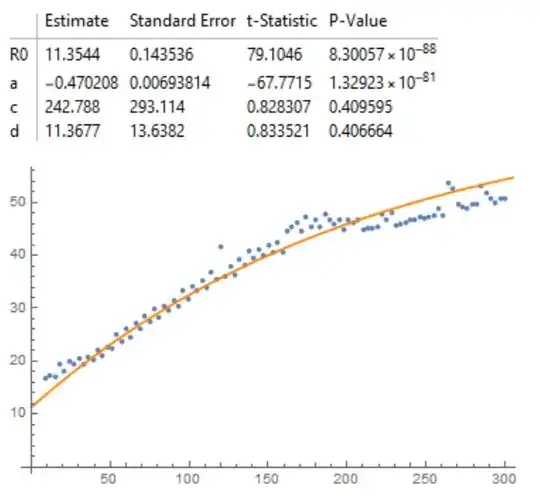
nlm["ParameterTable"]
Show[ListPlot[data], Plot[nlm[x], {x, 0, 310}, PlotStyle -> Orange]]
But I get something like that :
with errors like :
Encountered a gradient that is effectively zero. The result returned may not be a minimum; it may be a maximum or a saddle point.
How can I be better in the fit ?
Thx in advance