1

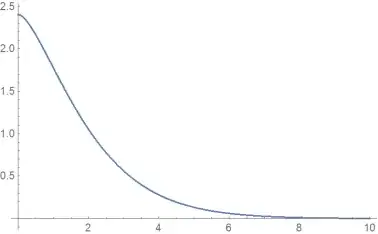
I am new in the use of Mathematica, so please forgive me..

I want to integrate and plot the following integral function:

$F(x)=\displaystyle\int_x^\infty\dfrac{t\sqrt{t^2-x^2}}{e^t-1}\text{d}t$:

where $x>0$ is the argument of my integral function.

Mathematica doesn't manage to do the calculation, not even if I substitute the x inside the square root with a number, e.g. 1.

Can anyone please help me? Thanks

Lele
  • 428
  • 2
  • 10

1 Answers1

4

Your problem can be solved numerically:

F[x_?NumericQ] :=NIntegrate[(t Sqrt[t^2 - x^2])/(Exp[t] - 1), {t, x, Infinity}]
Plot[F[x], {x, 0, 10}]

enter image description here

Ulrich Neumann
  • 53,729
  • 2
  • 23
  • 55
  • Thank you very much, it was silly I guess... Just a brief question: what is the meaning of using "?NumericQ" in the argument of the function? – Lele Apr 15 '19 at 14:21
  • @EmanueleCopello - Look at the documentation for PatternTest. Any function which uses numeric techniques such as NIntegrate can only evaluate if its argument(s) is/are numeric, so the argument(s) should be restricted to being numeric. – Bob Hanlon Apr 15 '19 at 16:16
  • Ok thank you. What if I have to evaluate it in this way: $F(x)=\sum_{j=1}^n\displaystyle\int_{x_j}^\infty\dfrac{t\sqrt{t^2-x_j^2}}{e^t-1}\text{d}t$ where $x_j$ should be a list of values I have to insert somehow... What is the best computational way to do it? – Lele Apr 16 '19 at 10:22
  • The sum(!) doesn't depend on x and therefor doesn't define F[x]! – Ulrich Neumann Apr 16 '19 at 10:31
  • Ok sorry, I have to specify that better.. My function is in fact this one:

    $F(T)=\displaystyle\sum_{j=1}^n\displaystyle\int_{m_j/T}^\infty\dfrac{t\sqrt{t^2-(m_j/T)^2}}{e^t-1}\text{d}t$

     – Lele Apr 16 '19 at 10:45
  • Ok, what's the reason not to calculate the single summands numerically as proposed in my answer? – Ulrich Neumann Apr 16 '19 at 11:12
  • Yeah I want to do that, but I would like to know how to manage the list of $m_j$ variables. I am supposing to sum lots of pieces and I would like not to rewrite the function every time, but just using some kind of list of values to sum on, as much as I would do in a for cycle with arrays and stuff like that... – Lele Apr 16 '19 at 14:23
  • I want to sum over something like

    F[x_?NumericQ] :=NIntegrate[(t Sqrt[t^2-(m[i]/x)^2])/(Exp[t] + 1)/(2*Zeta[3]), {t, m[i]/x, Infinity}]

    where m[i] is an array of values.. Can I define an array of functions like F[x,i] and then sum over i? It doesn't seem to work indeed...

     – Lele Apr 16 '19 at 15:27
  • Again the function you are asking for has changed...With the definition I gave in my answer you can solve the sum you called "F[T]": Total[Table[F[m[i]/T],{i,1,n}] – Ulrich Neumann Apr 16 '19 at 19:25