How to Make a Beautiful Stacked 3D Plot?

Question

I am looking to make a plot where:

Plot is composed of a group of 2D plots, stacked in 3D.
The height of the line is indicated by the color.
The mean of the wave of each plot is indicated by a dashed line to the axis.

How is this type of graph called?

Simplest / fastest way of doing something similar (less complex than in the image, I don't need 3 of those, and the black and white waveforms to the right etc.).

Related: https://mathematica.stackexchange.com/q/1413/1871 – xzczd Apr 18 '19 at 03:03 — xzczd, Apr 18 '19 at 03:03

Edmund · Answer 1 · 2019-04-18T01:21:15.887

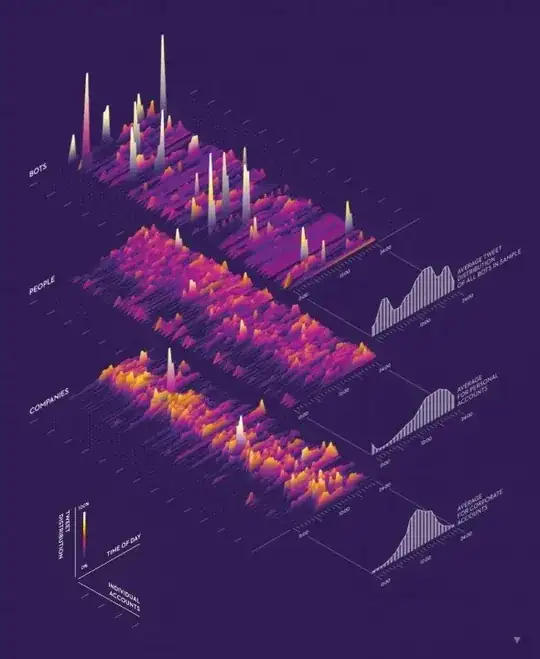
You may use ParametricPlot3D to do all of the heavy lifting.

With this method you first need the functions for each curve. I generate some data series with RandomVariate and then use SmoothKernelDistribution and PDF to obtain the function curves.

SeedRandom[987]
obs = RandomVariate[StudentTDistribution[3, 1, 5], {10, 20}];
foos = PDF@*SmoothKernelDistribution /@ obs;

Then

Plot[Through@foos@u, {u, -5, 10},
 ColorFunction -> ColorData["SunsetColors"],
 Background -> Lighter@Purple,
 AxesStyle -> White,
 TicksStyle -> White]

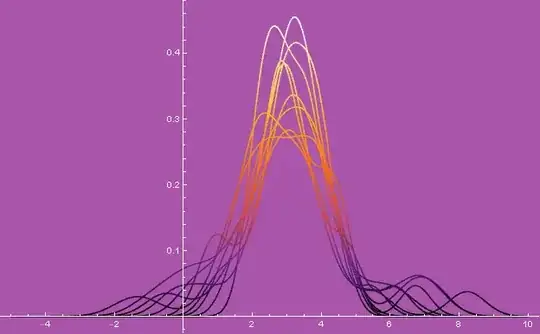
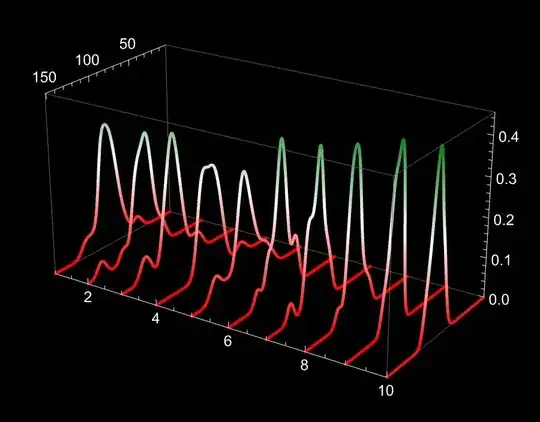
These functions can then be parameterised to create the curves in 3D with ParametricPlot3D.

ParametricPlot3D[
 MapIndexed[{First@#2, u, #1[u]} &]@foos, {u, -5, 10},
 BoxRatios -> {5, 1, 1},
 PlotRange -> Full,
 ColorFunction -> ColorData["SunsetColors"],
 Background -> Lighter@Purple,
 AxesStyle -> White,
 TicksStyle -> White,
 Boxed -> False,
 AxesEdge -> {{0, 0}, {1, 0}, {1, 1}},
 ViewPoint -> {3, -2, 1.5},
 ImageSize -> Large]

With a further parameterisation these curves can create 3D surfaces with ParametricPlot3D.

ParametricPlot3D[
 MapIndexed[{First@#2, u, v #1[u]} &]@foos, {u, -5, 10}, {v, 0, 1},
 BoxRatios -> {5, 1, 1},
 PlotRange -> Full,
 ColorFunction -> ColorData["SunsetColors"],
 Background -> Lighter@Purple,
 AxesStyle -> White,
 TicksStyle -> White,
 Boxed -> False,
 AxesEdge -> {{0, 0}, {1, 0}, {1, 1}},
 ViewPoint -> {3, -2, 1.5},
 ImageSize -> Large,
 Mesh -> None,
 PlotLegends -> Automatic,
 PlotPoints -> {80, 15},
 Ticks -> {{#, IntegerName@#} & /@ Range@10, Automatic, Automatic}]

The rest is reading up on ParametricPlot3D and Graphics3D options in the documentation to get the exact look you are seeking.

Hope this helps.

score 5 · Answer 2 · answered Apr 17 '19 at 17:15

These plots are very non-trivial to make (and there are no 'built-in' options as far as I am aware). You probably have to work directly with Graphics3D and Polygon for this, for example:

   polys = Table[
     Join[{{0, y, 0}}, 
     Table[{x, y, RandomReal[1]}, {x, 0, 10, .1}], {{10, y, 0}}],
     {y, 0, 10, 0.5}];

And then:

Graphics3D[{{Purple, 
   Polygon[{{0, 0, 0}, {0, 10, 0}, {10, 10, 0}, {10, 0, 0}}]},
  {EdgeForm[None], 
   Table[Polygon[poly, 
     VertexColors -> 
      Map[Blend[{Purple, White}, #] &, poly[[All, 3]]]], {poly, 
     polys}]}
  }, Lighting -> "Neutral", ImageSize -> Large, 
 BoxRatios -> {1, 2, .1}, Boxed -> False, Background -> Black, 
 ViewPoint -> {1.3, 2.4, 1.5}]

That will get you this far:

score 3 · Answer 3 · answered Nov 17 '23 at 10:55

Since V 12.3 we have ListLinePlot3D

Using Edmunds data we get

SeedRandom[987];
obs = RandomVariate[StudentTDistribution[3, 1, 5], {10, 20}];
foo = PDF @* SmoothKernelDistribution /@ obs;
ListLinePlot3D[
 Transpose @ Table[Through @ foo @ u, {u, -5, 10, 0.1}],
 AxesStyle -> White,
 TicksStyle -> White,
 Background -> Black,
 BoxRatios -> {1, 2, 1},
 ColorFunction -> "RedGreenSplit",
 ImagePadding -> 30,
 ViewPoint -> {3, 2, 1.5}]

How to Make a Beautiful Stacked 3D Plot?

3 Answers3