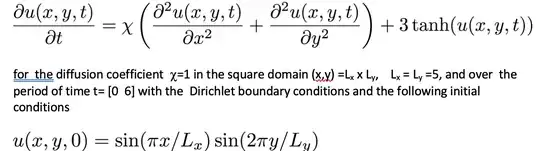Solving 2D Reaction-Diffusion with Explicit Euler Method

Question

I am trying to solve this following 2D-Diffusion equation (I wrote it in Word, so it looks nice)

(Note: I am solving this for a 100x100 mesh point)

I tried to solve the above equation using the following code:

s1 = NDSolve[{D[u[t, x, y], t] == 
D[u[t, x, y], x, x] + D[u[t, x, y], y, y] + 3*Tanh[u[t, x, y]], 
u[0, x, y] == Sin[(\[Pi] x)/5] Sin[(2 \[Pi] y)/5], 
u[t, -5, y] == 0, u[t, 5, y] == 0, u[t, x, -5] == 0, 
u[t, x, 5] == 0}, u, {t, 0, 6}, {x, -5, 5}, {y, -5, 5}, 
Method -> {"FixedStep", Method -> "ExplicitEuler"}, 
MaxStepFraction -> 10000, WorkingPrecision -> MachinePrecision]

This results in the consistent error of:

NDSolve::eerr
Warning: scaled local spatial error estimate of 26.30473550335526` at \
t = 6.` in the direction of independent variable x is much greater \
than the prescribed error tolerance. Grid spacing with 15 points may
be too large to achieve the desired accuracy or precision. A
singularity may have formed or a smaller grid spacing can be
specified using the MaxStepSize or MinPoints method options.

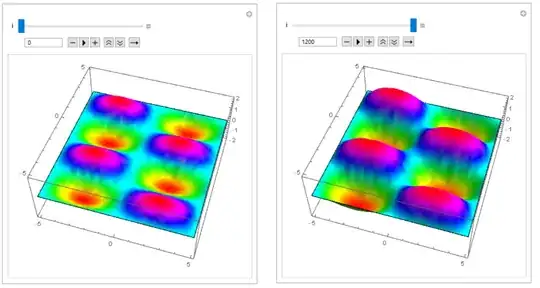
I also want to visualize the above equation in such a way that it is appropriate to show for a professional presentation (preferably as a movie)

This is the code that I came up with for the following problem:

a = Table[
Plot3D[u[t, x, y] /. s1, {x, -5, 5}, {y, -5, 5}, Mesh -> 100, 
PlotRange -> All, 
ColorFunction -> Function[{x, y, z}, Hue[.3 (1 - z)]]], {t, 0, 6}]

In summary, I cannot solve the above equation because of an error and I don't know how to visualize equations similar to it properly.

"What are the best practices when numerical solving PDEs in Mathematica?" Best practice is to not use explicit Euler because they require tiny time step sizes. It is much better to use implicit solvers. — Henrik Schumacher, Apr 22 '19 at 23:31
I actually used the very same code to approximate using 4th order Runge Kutta, and it worked fine. Funnily enough, the less robust method (Forward Euler) is refusing to work as highlighted in the post. The reason I am doing an Explicit Euler is to compare it with other numerical methods! Moreover, the question is meant to ask in terms of code as I feel I am always under Mathematica's will when I use NDSolve, and I want to know how to navigate its built-in AI. {Sorry for my bad English. I am not a native English speaker!} — H. Alanzi, Apr 22 '19 at 23:37
@H.Alanzi if you edit the question to be more concise and request that which you desire, it will be easier to find it offered in an answer. I am curious about the outcomes, so this is my recommendation — CA Trevillian, Apr 23 '19 at 08:00
Alright. I will edit it shortly. Any specific edit in particular? — H. Alanzi, Apr 23 '19 at 19:54

score 4 · Accepted Answer · answered Apr 24 '19 at 06:43

Rule of thumb: if NDSolve doesn't work well on solving PDE, usually the problem lies in spatial discretization.

When solving spatially 2D problem, the default grid points in each spatial dimension of TensorProductGrid is 15, which may be a bit small in many cases. So let's make the grid denser:

sref = NDSolveValue[{D[u[t, x, y], t] == 
    D[u[t, x, y], x, x] + D[u[t, x, y], y, y] + 3*Tanh[u[t, x, y]], 
   u[0, x, y] == Sin[(π x)/5] Sin[(2 π y)/5], u[t, -5, y] == 0, u[t, 5, y] == 0, 
   u[t, x, -5] == 0, u[t, x, 5] == 0}, u, {t, 0, 6}, {x, -5, 5}, {y, -5, 5}, 
  Method -> {"MethodOfLines", 
    "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> 50, 
      "MinPoints" -> 50, "DifferenceOrder" -> 4}}]; //AbsoluteTiming
(* {0.601145, Null} *)

The problem is solved without warning. ExplicitEuler can be used of course. We just need to make the StartingStepSize small enough.

s1 = NDSolveValue[{D[u[t, x, y], t] == 
    D[u[t, x, y], x, x] + D[u[t, x, y], y, y] + 3*Tanh[u[t, x, y]], 
   u[0, x, y] == Sin[(π x)/5] Sin[(2 π y)/5], u[t, -5, y] == 0, u[t, 5, y] == 0, 
   u[t, x, -5] == 0, u[t, x, 5] == 0}, u, {t, 0, 6}, {x, -5, 5}, {y, -5, 5}, 
  Method -> {"MethodOfLines", 
    "SpatialDiscretization" -> {"TensorProductGrid", "MaxPoints" -> 50, 
      "MinPoints" -> 50, "DifferenceOrder" -> 4}, 
    Method -> {"FixedStep", Method -> "ExplicitEuler"}}, 
  StartingStepSize -> {0.007, Automatic, Automatic}]; //AbsoluteTiming
(* {0.833146, Null} *)
Plot[{s1[t, 1, 1], sref[t, 1, 1]}, {t, 0, 6}, PlotStyle -> {Automatic, {Thick, Dashed}}]

Animation is easy:

ListAnimate@
 Table[Plot3D[s1[t, x, y], {x, -5, 5}, {y, -5, 5}, PlotRange -> 2], {t, 0, 1, 1/25}]

score 2 · Answer 2 · answered Apr 23 '19 at 23:06

2

I can offer this implementation explicitly Euler

Lx = 5; Ly = 5; h = .1; t0 = h^2/2; n = 1200;
reg = DiscretizeRegion[Rectangle[{-Lx, -Ly}, {Lx, Ly}], 
  MaxCellMeasure -> h]
Us[0][x_, y_] := Sin[Pi*x/Lx]*Sin[2*Pi*y/Ly]
Do[Us[i] = 
    NDSolveValue[{(u[x, y] - Us[i - 1][x, y])/t0 == 
       D[u[x, y], x, x] + D[u[x, y], y, y] + 3*Tanh[Us[i - 1][x, y]], 
      DirichletCondition[u[x, y] == 0, True]}, 
     u, {x, y} \[Element] reg], {i, 1, n}]; // AbsoluteTiming
Manipulate[
 Plot3D[Us[i][x, y], {x, y} \[Element] reg, Mesh -> None, 
  ColorFunction -> Hue, PlotRange -> {-2, 2}], {i, 0, n, 10}]

answered Apr 23 '19 at 23:06

Alex Trounev

44,369
3
48
106

Thank you for this! I was wondering if there is a way to make this code quicker? As it does take a while to compute. – H. Alanzi Apr 24 '19 at 03:44
@H.Alanzi You can make the code faster by using Assemble[]. See Henrik Schumacher post at https://mathematica.stackexchange.com/questions/193700/how-to-diminish-computation-time-when-nonlinearity-appears-in-2d-heat-conduction/193766#193766 – Alex Trounev Apr 24 '19 at 10:55
We can also make the code faster by putting h=.2; n=300, as in answer @xzczd – Alex Trounev Apr 24 '19 at 11:15

Solving 2D Reaction-Diffusion with Explicit Euler Method

2 Answers2

Linked