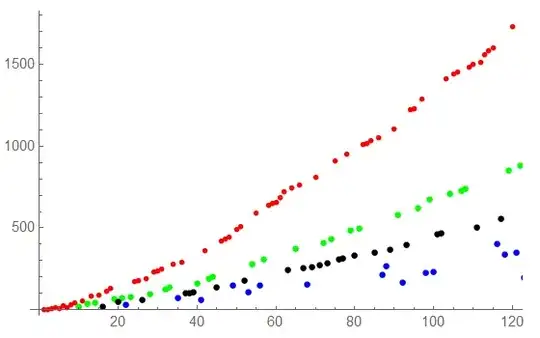
I have a sequence that forms visible lines when plotted as a graph, what would be a good way to automatically partition the sequence to create a list of sequences, one for each line that is visible when the sequence is plotted?
Here is the start of the sequence:
list = {2,3,5,11,7,23,13,29,41,17,53,37,83,43,89,19,113,131,67,47,73,31,79,173,179,61,191,97,233,239,251,127,139,281,71,293,101,103,107,163,59,359,193,199,137,419,431,443,151,491,509,181,109,277,593,149,307,641,653,659,683,719,241,743,373,761,257,157,263,809,271,409,283,433,911,311,313,953,487,331,499,1013,1019,1031,347,1049,211,269,367,1103,577,167,397,1223,1229,619,1289,223,673,229,461,467,1409,709,1439,1451,727,739,1481,1499,503,1511,1559,1583,1601,401,557,337,853,1733,349,883,197};
Thanks.
cheers, Jamie