This is how you define the function $g$ in Mathematica:
g[a_, x_] = a*Sin[π*x];
Making a color-plot of the function $g(g(g(x)))-x$ in the $a$-$x$ plane and indicating the zero-contours, we see the lobes of 3-cycles:
DensityPlot[g[a, g[a, g[a, x]]] - x, {a, 0, 1}, {x, 0, 1},
MeshFunctions -> {#3 &}, Mesh -> {{0}}, PlotPoints -> 100]

Now we know where they all are, find a 3-cycle for a specific value of $a$:
With[{a = 0.95},
x3 = x /. FindRoot[g[a, g[a, g[a, x]]] == x, {x, 0.2}];
{{x3, g[a, x3], g[a, g[a, x3]], g[a, g[a, g[a, x3]]]},
Abs[D[g[a, g[a, g[a, x]]], x]] /. x -> x3}]
{{0.201558, 0.562152, 0.931948, 0.201558}, 4.06318}
Oops, this is an unstable 3-cycle as the derivative (last number) is larger than 1 in magnitude (thanks @march!). Try again:
With[{a = 0.94},
x3 = x /. FindRoot[g[a, g[a, g[a, x]]] == x, {x, 0.15}];
{{x3, g[a, x3], g[a, g[a, x3]], g[a, g[a, g[a, x3]]]},
Abs[D[g[a, g[a, g[a, x]]], x]] /. x -> x3}]
{{0.176489, 0.494893, 0.939879, 0.176489}, 0.345007}
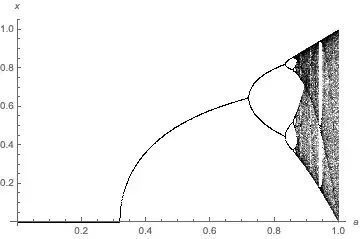
This time it worked: we found a stable 3-cycle $0.176489, 0.494893, 0.939879$ at $a=0.94$.
Let's make a new plot where the cycle contours are only shown in the stable regions (i.e., only stable 3-cycles):
g3[a_, x_] = Nest[g[a, #] &, x, 3];
dg3[a_, x_] = D[g3[a, x], x];
DensityPlot[g3[a, x] - x, {a, 0, 1}, {x, 0, 1},
MeshFunctions -> {#3 &}, Mesh -> {{0}}, MeshStyle -> Red,
PlotPoints -> 100,
RegionFunction -> Function[{a, x, f}, Abs[dg3[a, x]] <= 1]]

Zooming in on one of the regions of stable 3-cycles:

The two black dots that mark the limits of the stable 3-cycle band are found with
Q1 = {a, x} /. FindRoot[{g3[a, x] == x, dg3[a, x] == 1}, {{a, 0.94}, {x, 0.5}}]
{0.937818, 0.5152}
Q2 = {a, x} /. FindRoot[{g3[a, x] == x, dg3[a, x] == -1}, {{a, 0.94}, {x, 0.5}}]
{0.942488, 0.485444}
The region of stable 3-cycles is therefore $a\in[0.937818, 0.942488]$.