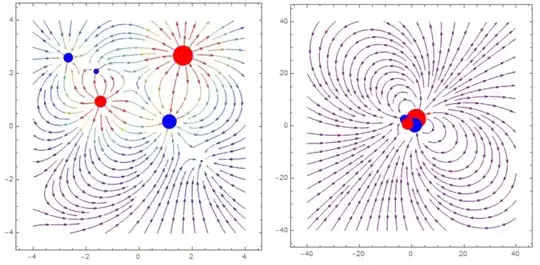
I want to show an electric field of several arrangements of point charges in xy-plane. I wrote a routine that plots an electric field of a charge:
r0 = {a, b};
r1 = {-a, b};
r2 = {-a, -b};
r2 = {-a, -b};
pot[r_] := q/Norm[r - r0] + q/Norm[r - r2] - q/Norm[r - r1] - q/Norm[r - r3]
fld[r_] := (q*(r - r0)/Norm[r - r0]^3 + q*(r - r2)/Norm[r - r2]^3 - q*(r - r1)/Norm[r - r1]^3 - q*(r - r3)/Norm[r - r3]^3)
a = 2.5;
b = 2.5;
q = 1;
StreamPlot[fld[{x, y}], {x, 0, 5}, {y, 0, 5},PlotRangePadding -> None, FrameLabel -> "electric field",Epilog -> {Red, Disk[r0, 0.07], Blue , Line[{{0, 5.5}, {0, 0}, {5.5, 0}}]}]
Now I want to show:
a) 2 charges with inverted sign
b) 4 charges on edges of a cuboid in xy-plane (edges connect charges with inverted sign)
c) 6 randomly distributed charges with vanishing total charge by using RandomReal and initialize random generator with SeedRandom[1234567]
Could someone help me out with a,b,c ? Thank you very much!