I would like to draw a quadrilateral inscribed within a circle. How can I construct this figure, taking into account arbitrary (specified) side lengths, while still ensuring that the vertices of the quadrilateral lie on the circle?
Asked
Active
Viewed 1,520 times
2
-
It is to be quad in a circle with a user-specified length of the side of a quad, is to change the circle to fit a quad in a circle. – user5955 Feb 18 '13 at 13:12
-
Just that, given the length of the side of the square will fit within a circle, which is automatically size to fit the square. – user5955 Feb 18 '13 at 13:21
-
I have edited your question according to what I think it means. Can you confirm whether or not this is correct? – Oleksandr R. Feb 18 '13 at 13:24
-
Yes, it is correct Oleksandr R – user5955 Feb 18 '13 at 13:28
-
A circle is defined by three (non-identical, not collinear) points. A fourth point cannot be arbitrarily chosen... – Yves Klett Feb 18 '13 at 13:31
-
@OleksandrR. Inscribing is not compatible with hitting the vertices of the inscribed polygon... – Yves Klett Feb 18 '13 at 13:32
-
3Perhaps http://mathworld.wolfram.com/CyclicQuadrilateral.html ? – cormullion Feb 18 '13 at 13:37
-
@YvesKlett I know, but I couldn't deduce from the question how many side lengths are to be specified. I can't guess what the OP wants, so I only edited for comprehensibility, not necessarily logical consistency. :) – Oleksandr R. Feb 18 '13 at 13:38
-
@OleksandrR. you´re between a rock and a hard place there :P – Yves Klett Feb 18 '13 at 13:39
-
mathworld.wolfram.com/CyclicQuadrilateral.html Yes 1 picture – user5955 Feb 18 '13 at 13:40
-
2@user5955 You image showed a rectangular inscribed. Therefore, I assumed you don't need an arbitrary quadrilateral. – halirutan Feb 18 '13 at 13:52
1 Answers
7
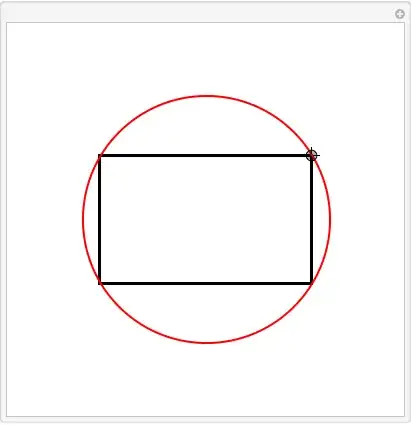
I hope I understood your question correctly.
When you place your figure at {0,0}, meaning the center of the circle and the center of the rectangle is there, you don't need to calculate very much. Indeed, everything is then fixed by exactly one point p defining a corner of the rectangle and the radius of the circle.
A dynamic version of your graphics can be written down in only a few lines of code
Manipulate[
Graphics[{FaceForm[None], EdgeForm[Thick], Rectangle[-p, p],
Thick, Red, Circle[{0, 0}, Norm[p]]}, PlotRange -> {{-2, 2}, {-2, 2}}],
{{p, {1, 1}}, Locator}
]
halirutan
- 112,764
- 7
- 263
- 474