Minimum path on a rectangular prism

Question

First of all, this is a fun question that I have seen from here. We have a rectangular prism with dimension $30\times12\times12$ cubic inches. Assume that there is an ant at the blue point 1 inch above from $xy$ plane and mid point of $y$ direction, i.e. coordinate of ant is $(30,6,1)$ and there is some honey at red point 11 inch above from $xy$ plane and mid point of $y$ direction, i.e. coordinate of honey is $(0,6,11)$. Question: What is the minimum path that ant reaches to honey? I thought I could solve it using Mathematica. Here is my starting point.

Graphics3D[{Opacity@0.5, Cuboid[{0, 0, 0}, {30, 12, 12}], Red, 
  Sphere[{0, 6, 11}, 0.5], Blue, Sphere[{30, 6, 1}, 0.5]}, 
 Boxed -> False]

Best I can do is this:

pInitial = {30, 6, 1};
p1 = {30, 0, z};
p2 = {x, 0, 12};
p3 = {0, y, 12};
pFinal = {0, 6, 11};

f = EuclideanDistance[pInitial, p1] + EuclideanDistance[p1, p2] + 
  EuclideanDistance[p2, p3] + EuclideanDistance[p3, pFinal]

$f(x,y,z)=\sqrt{\left| x\right| ^2+\left| y\right| ^2}+\sqrt{\left| 30-x\right| > ^2+\left| z-12\right| ^2}+\sqrt{\left| y-6\right| ^2+1}+\sqrt{\left| > 1-z\right| ^2+36}$

sol = NMinimize[f, {x, y, z}]

{40.7185, {x -> 12.0591, y -> 5.54055, z -> 3.75679}}

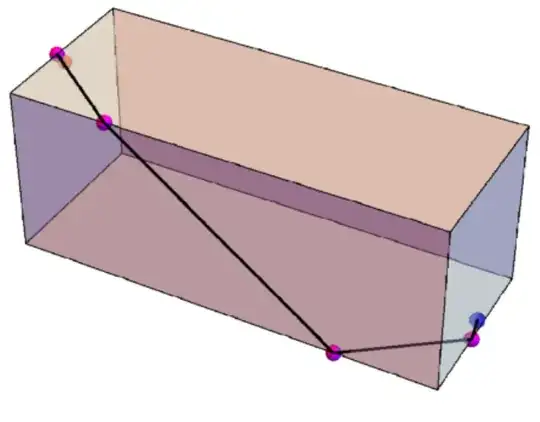
With[{p1 = p1 /. Last@sol, p2 = p2 /. Last@sol, p3 = p3 /. Last@sol}, 
 Graphics3D[{Opacity@0.5, Cuboid[{0, 0, 0}, {30, 12, 12}], Red, 
   Sphere[{0, 6, 11}, 0.5], Blue, Sphere[{30, 6, 1}, 0.5], Opacity@1, 
   Black, Thick, 
   Line /@ {{pInitial, p1}, {p1, p2}, {p2, p3}, {p3, pFinal}}, 
   Magenta, Sphere[#, 0.5] & /@ {p1, p2, p3}}, Boxed -> False]]

Answer 1

Here is the solution: No need unfolding. welcome to different approaches.

pInitial = {30, 6, 1};
p1 = {30, y1, 0};
p2 = {x1, 0, 0};
p3 = {x2, 0, 12};
p4 = {0, y2, 12};
pFinal = {0, 6, 11};
f = EuclideanDistance[pInitial, p1] + EuclideanDistance[p1, p2] + 
  EuclideanDistance[p2, p3] + EuclideanDistance[p3, p4] + 
  EuclideanDistance[p4, pFinal]

$f(x_1,x_2,y_1,y_2)=\sqrt{\left| x_1-x_2\right| ^2+144}+\sqrt{\left| 30-x_1\right| ^2+\left| y_1\right| ^2}+\sqrt{\left| x_2\right| ^2+\left| y_2\right| ^2}\\+\sqrt{\left| 6- y_1\right| ^2+1}+\sqrt{\left| y_2-6\right| ^2+1}$

sol = NMinimize[f, {x1, x2, y1,y2}]

{40., {x1 -> 23., x2 -> 7.00005, y1 -> 5.25001, y2 -> 5.25001}}

 With[{}, {p1, p2, p3, p4} = {p1, p2, p3, p4} /. Last@sol; 
 Graphics3D[{Opacity@0.5, Cuboid[{0, 0, 0}, {30, 12, 12}], Red, 
   Sphere[{0, 6, 11}, 0.5], Blue, Sphere[{30, 6, 1}, 0.5], Opacity@1, 
   Black, Thick, 
   Line /@ {{pInitial, p1}, {p1, p2}, {p2, p3}, {p3, p4}, {p4, 
      pFinal}}, Magenta, Sphere[#, 0.5] & /@ {p1, p2, p3, p4}}, 
  Boxed -> False]]