It seems like a natural thing to do, however I can't seem to find anything on the docs nor here on SE.
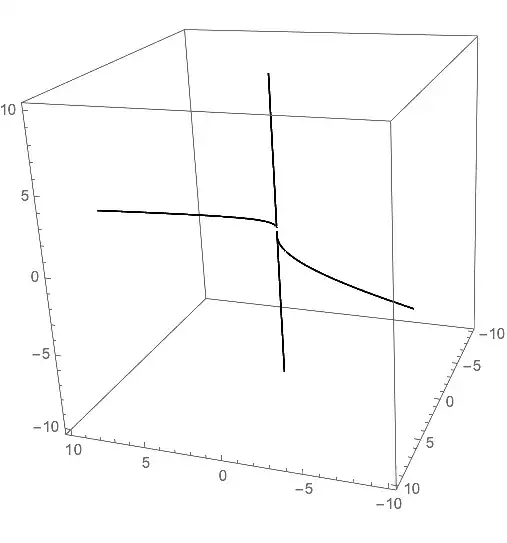
What I'd like to plot is the locus of solutions to a system of (polynomial) equations, e.g. $$\begin{cases}x=yz\\ y^2=xz\end{cases}$$.
I tried with with the command
ContourPlot3D[{x == y*z, y^2 == x*z}, {x, -10, 10}, {y, -10, 10}, {z, -10, 10}]
However I get the two plots of each equation, which is not what I want:

Basically, I'd like to see just the intersection.
What is the easiest way to do that?