Eigenvalues broken in Version 12.0

Question

Bug introduced in 12.0 and fixed in 12.1

---

The following code calculates the eigenvalues of a certain complex matrix, which come in pairs of opposite complex numbers. Therefore one can check whether the sum of all eigenvalues is equal to the trace of the matrix, which is zero.

This is indeed the case in Version 10.1 & 11.3 as far as I tested. However, Version 12.0 (Windows, Mac, Linux) gives something seriously wrong.

NN = 374; R = 0.05;
t1 = -1 + Cos[x] - I Sin[x] + I R; t1p = -1 + Cos[x] + I Sin[x] + 
  I R;
mat[x_] = 
  DiagonalMatrix[Table[If[EvenQ[n], t1, -1], {n, 0, 2 NN - 1 - 1}], 
    1] + DiagonalMatrix[
    Table[If[EvenQ[n], t1p, -1], {n, 0, 2 NN - 1 - 1}], -1] + 
   DiagonalMatrix[Table[If[EvenQ[n], -1, 0], {n, 0, 2 NN - 1 - 3}], 
    3] + DiagonalMatrix[
    Table[If[EvenQ[n], -1, 0], {n, 0, 2 NN - 1 - 3}], -3];
mat0 = mat[-0.2 \[Pi]];
Tr@mat0  (* 0. *)
Total@Eigenvalues@mat0  (* 0.394003 - 0.566499 I *)

I would rather switch back to 11.3 for a while. This looks really dangerous...

---

Original post of a more complex matrix with the same issue:

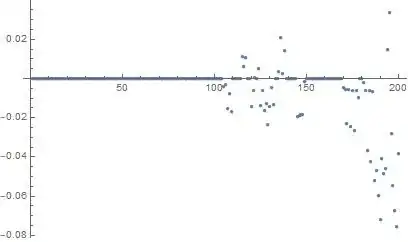
The code plots the real part of adding each pair. So the correct plot should be just zeros everywhere. This is the case in Version 10.1 & 11.3 as far as I tested (scattered numbers around $10^{-14}$ or so). However, Version 12.0 (Windows, Mac, Linux) gives something different as shown below.

NN = 200; R = 0.05;
xlist = Table[x, {x, -0.2 \[Pi], 0.2 \[Pi], 0.01}];
modl[n_] := 2*^-3 (Quotient[n, 2] - NN/2);
t1 = -1 + Cos[x] - I Sin[x] + I R; t1p = -1 + Cos[x] + I Sin[x] + I R;
t2a[n_] := -1 - modl[n]; t2b[n_] := -1 + modl[n];
mat[x_] = 
  DiagonalMatrix[
    Table[If[EvenQ[n], t1, t2a[n]], {n, 0, 2 NN - 1 - 1}], 1] + 
   DiagonalMatrix[
    Table[If[EvenQ[n], t1p, t2a[n]], {n, 0, 2 NN - 1 - 1}], -1] + 
   DiagonalMatrix[
    Table[If[EvenQ[n], t2b[n], 0], {n, 0, 2 NN - 1 - 3}], 3] + 
   DiagonalMatrix[
    Table[If[EvenQ[n], t2b[n], 0], {n, 0, 2 NN - 1 - 3}], -3];
list0 = Sort@Re@Eigenvalues[mat[xlist[[3]]]];
list0p = Table[list0[[i]] + list0[[2 NN - i + 1]], {i, NN}];
ListPlot[Tooltip@list0p, PlotRange -> All]

Answer 1

Not a solution but too big for a comment. There seems to be a catastrophic failure in Eigenvalues happening that is not due to the matrix being crazy. As a diagnostic, let's calculate the smallest (by absolute value) eigenvalue of the upper-left $n\times n$ part of the matrix

M = mat[xlist[[3]]];

For odd $n$ the answer is zero, so let's only do this for even $n$. We do this in two ways

1. Calculate all eigenvalues and pick the one with the smallest absolute value:

    e1[n_?EvenQ] := M[[;; n, ;; n]] // Eigenvalues // Abs // Min

2. Calculate only the smallest eigenvalue (by absolute value) with the Arnoldi algorithm:

    e2[n_?EvenQ] := Eigenvalues[M[[;; n, ;; n]], 1, 
      Method -> {"Arnoldi", "Criteria" -> "Magnitude", "Shift" -> 0}] // First // Abs

Method (2) is very reliable, whereas method (1) breaks down for $n=358$ and above:

Considering that the Arnoldi algorithm has no problems with this matrix, there seems to be something really strange going on in method 1.

$Version
(* 12.0.0 for Mac OS X x86 (64-bit) (April 7, 2019) *)

Answer 2

Edit: Eigensystem fixed in 12.1 in addition to Eigenvalues

I attempted a workaround, to see if Eigensystem had any issues also. It does. This is very unfortunate.

(Will we have to wait for 12.1 for the fix (?!))
(We waited for 12.1 for the fix (!!))

My code here:

e3[n_?EvenQ] := Eigensystem[M[[;; n, ;; n]]][[1]] // Abs // Min

Produces the following, which matches with @Roman shows:

(Apologies the colors/styles don't match with the plot from @Roman !!)

$Version
(* 12.0.0 for Microsoft Windows (64-bit) (April 6, 2019) *)

Answer 3

Fixed in 12.1

---

---

ClearAll[x, n];
NN = 374; R = 0.05;
t1 = -1 + Cos[x] - I Sin[x] + I R; t1p = -1 + Cos[x] + I Sin[x] + I R;
mat[x_] = 
  DiagonalMatrix[Table[If[EvenQ[n], t1, -1], {n, 0, 2 NN - 1 - 1}], 
    1] + DiagonalMatrix[
    Table[If[EvenQ[n], t1p, -1], {n, 0, 2 NN - 1 - 1}], -1] + 
   DiagonalMatrix[Table[If[EvenQ[n], -1, 0], {n, 0, 2 NN - 1 - 3}], 
    3] + DiagonalMatrix[
    Table[If[EvenQ[n], -1, 0], {n, 0, 2 NN - 1 - 3}], -3];
mat0 = mat[-0.2 \[Pi]];
Tr@mat0  (*0.*)
(Total@Eigenvalues@mat0) // Chop

Answer 4

I am not qualified to be at this site because the last time I used eigenvectors was well over half a century ago. The word "stiff matrix" came back to me, so I increased the precision of the author's code by rounding the two real numbers to 50 places. It took forever to compute, but Mathematica solved the problem accurately. That is, R = N[5/100, 50]; and mat0 = mat[N[-2/10 [Pi], 50]]; I ended up with zero to 47 places.

Occasionally--when solving differential equations numerically--I came across stiff systems, so I checked for this condition prior to working with them (I forget the method I used).

Again, sorry for my layman's interjection.

Nick Bagley