4

I am trying to code the following integral equation to find the solution numerically using Mathematica.

First we define the following functions:

phi[x_]:=Piecewise[{{1, 0 < x < 1}}, 0]

psi1[x_] := (phi[2 x-1] - phi[2 x]);

psijk[x_, j_, k_] := (Sqrt[2])^j psi1[-2^j x - k]

f[x_] := 1/1155 (112 (-1 + x)^(3/4) + x (144 (-1 + x)^(3/4) + x (1155 + 256 (-1 + x)^(3/4) - 1280 x^(3/4) - (1155 + 512 (-1 + x)^(3/4)) x + 1024 x^(7/4))));

exactsoln[x_] := x^2 (1 - x);

I am trying to solve the following integral equation for u (x) (numerically). where 

u[x] + Integrate[(x - t)^(-1/4)*u[t], {t, 0, x}] - 
   Integrate[(x - t)^(-3/4)*u[t], {t, 0, 1}] = f[x];

where f[x] is defined as above. Here is the numerical scheme. The approximated solution \approx[x] which can be written as

approxsoln[x_, n_] := 
 Sum[c[j, k]*psijk[x, j, k], {j, 0, n}, {k, -2^n, 2^n - 1}]

Then, we will end up by

Sum[c[j, k]*(psijk[x, j, k] - 
     Integrate[(x - t)^(-1/4)* psijk[t, j, k], {t, 0, x}] - 
     Integrate[(x - t)^(-1/4)* psijk[t, j, k], {t, 0, 1}]), {j, 0, n}, {k, -2^n, 2^n - 1}];

I think it is worth to try for n=10 first.

Mutaz
  • 323
  • 1
  • 6
  • 1
    Where to find the definition psijk[t, j, k] – Ulrich Neumann May 22 '19 at 06:25
  • @Ulrich Neumann Thank you. I have added it in the question and here it is for you psi1[x_] := (phi[2 x] - phi[2 x - 1]);psijk[x_, j_, k_] := Piecewise[{{(Sqrt[2])^j psi1[2^j x - k], 0 <= j}, {2^j psi1[2^j (x - k)], j < 0}}] – Mutaz May 22 '19 at 06:30
  • I tried to Plot[f[x],{x,0,1}] , but nothing is plotted. Probably f[x]is wrong, perhaps (-1+x)^... has to be substituted by (1-x)^..? Also I suppose an error in the integral equation, I think it should be u[x] - Integrate[(x - t)^(-1/4)*u[t], {t, 0, x}] - Integrate[(t-x)^(-1/4)*u[t], {t, x, 1}] = f[x]; – Ulrich Neumann May 22 '19 at 14:30
  • 1
    Possible duplicate of Numerical solution of a singular integral equation – AccidentalFourierTransform May 22 '19 at 16:57
  • Different as the numerical scheme – Mutaz May 22 '19 at 20:23
  • 1
    @Mutaz Please check f[x] and your integral equation (see my comment). Therewith I could provide you a solution based on Galerkin method... – Ulrich Neumann May 23 '19 at 07:46
  • @ Ulrich Neumann It is true. Both side of the integral equations have complex values so you will not be able to plot f[x]. However, why you need to do so, I think you don't need to plot f. The most important is the exact solution as long as it satisfied both side of the integral equation. Waiting your contribution, though! – Mutaz May 23 '19 at 07:55

2 Answers2

4

The numerical method I suggested here also works for this case.It uses expression describing the integral Integrate[(x - t)^(-1/4),t]

f[x_] := 1/
    1155 (112 (-1 + x)^(3/4) + 
     x (144 (-1 + x)^(3/4) + 
        x (1155 + 256 (-1 + x)^(3/4) - 
           1280 x^(3/4) - (1155 + 512 (-1 + x)^(3/4)) x + 
           1024 x^(7/4))));
ker[t_, x_] := -(4/3) (-t + x)^(3/4)

np = 101; points = fun = Table[Null, {np}];
Table[points[[i]] = i/np, {i, np}];
sol = Unique[] & /@ points;
Do[fun[[i]] = f[t] /. t -> points[[i]], {i, np}]; sol1 = 
 sol /. First@
   Solve[Table[
     sol[[j]] - 
       Sum[.5*(sol[[i]] + 
           sol[[i + 1]])*(ker[points[[i + 1]], points[[j]]] - 
           ker[points[[i]], points[[j]]]), {i, 1, np - 1}] - 
       Sum[.5*(sol[[i]] + 
           sol[[i + 1]])*(ker[points[[i + 1]], points[[j]]] - 
           ker[points[[i]], points[[j]]])*If[i >= j, 0, 1], {i, 1, 
         np - 1}] == fun[[j]], {j, 1, np}], sol];
u = Transpose[{points, Re[sol1]}];
Show[Plot[x^2*(1 - x), {x, 0, 1}, AxesLabel -> {"x", "u"}, 
  PlotStyle -> Blue], ListPlot[u, PlotStyle -> Orange]]

fig1

If we use the algorithm that @Mutaz offers, then a solution for n = 2 (for n = 5, a supercomputer is needed) looks like that

phi[x_] := Piecewise[{{1, 0 <= x < 1}}, 0]
psi1[x_] := (phi[2 x] - phi[2 x - 1]);
psijk[x_, j_, k_] := 
 Piecewise[{{(Sqrt[2])^j psi1[2^j x - k], 
    0 <= j}, {2^j psi1[2^j (x - k)], j < 0}}]
f[x_] := 1/
    1155 (112 (-1 + x)^(3/4) + 
     x (144 (-1 + x)^(3/4) + 
        x (1155 + 256 (-1 + x)^(3/4) - 
           1280 x^(3/4) - (1155 + 512 (-1 + x)^(3/4)) x + 
           1024 x^(7/4))));
exactsoln[x_] := x^2 (1 - x);
(*u[x]-Integrate[(x-t)^(-1/4)*u[t],{t,0,x}]-Integrate[(x-t)^(-1/4)*u[\
t],{t,0,1}]=f[x];*)
sol[x_, n_] := 

Sum[c[j, k]*psijk[x, j, k], {j, -n, n}, {k, -2^n, 2^n - 1}]
     n = 2;  var = 
     Flatten[Table[c[j, k], {j, -n, n, 1}, {k, -2^n, 2^n - 1, 1}]];np = 
     Length[var]; points = 
     Table[Null, {np}];
    Table[points[[i]] = i/np, {i, np}];
eq = ParallelTable[
    sol[points[[i]], n] - 
      Integrate[(points[[i]] - t)^(-1/4)*sol[t, n], {t, 0, 
        points[[i]]}] - 
      Integrate[(points[[i]] - t)^(-1/4)*sol[t, n], {t, 0, 1}] == 
     f[points[[i]]], {i, 1, np}]; 
{b, m} = N[CoefficientArrays[eq, var]];
sol1 = LinearSolve[m, -b];
u = Sum[c[j, k]*psijk[x, j, k], {j, -n, n}, {k, -2^n, 2^n - 1}] /. 
   Table[var[[i]] -> sol1[[i]], {i, Length[var]}];
Show[Plot[x^2*(1 - x), {x, 0, 1}, AxesLabel -> {"x", "u"}, 
  PlotStyle -> Blue, PlotLabel -> Row[{"n = ", n}]], 
 Plot[Re[u], {x, 0, 1}, PlotStyle -> Orange]]

fig2

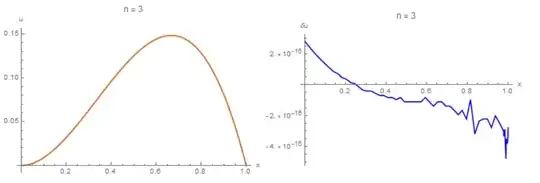
I will show another method that is in the middle position between what Roman suggested and what the author wants. This method is very accurate.Figure 3 on the right shows the difference between the exact solution and the numerical one with 'n = 3'. This difference is of the order of $10^{-16}$.

psijk[x_, j_] := x^j
f[x_] := 1/
    1155 (112 (-1 + x)^(3/4) + 
     x (144 (-1 + x)^(3/4) + 
        x (1155 + 256 (-1 + x)^(3/4) - 
           1280 x^(3/4) - (1155 + 512 (-1 + x)^(3/4)) x + 
           1024 x^(7/4))));
exactsoln[x_] := x^2 (1 - x);
(*u[x]-Integrate[(x-t)^(-1/4)*u[t],{t,0,x}]-Integrate[(x-t)^(-1/4)*u[\
t],{t,0,1}]=f[x];*)

sol[x_, n_] := Sum[c[j]*psijk[x, j], {j, 0, n}]

n = 3; var = Flatten[Table[c[j], {j, 0, n, 1}]]; np = 
 Length[var]; points = Table[Null, {np}];
Table[points[[i]] = i/np, {i, np}];
eq = ParallelTable[
    sol[points[[i]], n] - 
      Integrate[(points[[i]] - t)^(-1/4)*sol[t, n], {t, 0, 
        points[[i]]}] - 
      Integrate[(points[[i]] - t)^(-1/4)*sol[t, n], {t, 0, 1}] == 
     f[points[[i]]], {i, 1, np}]; // AbsoluteTiming

{b, m} = N[CoefficientArrays[eq, var]];
sol1 = LinearSolve[m, -b];


u = Sum[c[j]*psijk[x, j], {j, 0, n}] /. 
   Table[var[[i]] -> sol1[[i]], {i, Length[var]}];
Show[Plot[x^2*(1 - x), {x, 0, 1}, AxesLabel -> {"x", "u"}, 
  PlotStyle -> Blue, PlotLabel -> Row[{"n = ", n}]], 
 Plot[Re[u], {x, 0, 1}, PlotStyle -> Orange]]
Plot[x^2*(1 - x) - Re[u], {x, 0, 1}, AxesLabel -> {"x", "\[Delta]u"}, 
 PlotStyle -> Blue, PlotLabel -> Row[{"n = ", n}]]

fig3

Alex Trounev
  • 44,369
  • 3
  • 48
  • 106
4

Sorry, a little bit late...

This answer shows how to use Galerkin's Method to solve the integral equation.

ansatz: 

g[x_] := Table[x^i, {i, 0, 4}] (* Polynombasis *)
ui = Array[U, Length[g[x]], 0] (* ansatz: u[x]== ui.g[x] *)

system matrix (weighted residuals)

M = NIntegrate[Outer[Times, g[x], g[x]], {x, 0, 1}] -
NIntegrate[Outer[Times, g[x], g[t]]/(x - t)^(1/4), {x, 0, 1}, {t, 0, x},Exclusions -> {t == x}] -
NIntegrate[Outer[Times, g[x], g[t]]/(x - t)^(1/4), {x, 0, 1}, {t, 0, 1},Exclusions -> {t == x}]

=> left hand side of the discretized integral equation: M.ui

right hand side (of the discretized integral equation): rS

f[x_] := 1/ 1155 (112 (-1 + x)^(3/4) + x (144 (-1 + x)^(3/4) + x (1155 + 256(-1 + x)^(3/4) - 1280 x^(3/4) - (1155 + 512 (-1 + x)^(3/4)) x + 1024 x^(7/4))))
rS= NIntegrate[f[x] g[x], {x, 0, 1}]

=>=> approximation of the solution u[x]=(Inverse[M].rS).g[x]

p=LinearSolve[M,rS] 
Plot[Re[p].g[x], {x, 0, 1}]

enter image description here

That's it!

Thereby the basis functions can easily be changed, for example to piecewise trianglefunctions. Besides in this example the integration can be done analytically.

addendum

With wavelet-basis:

g[x_] := Table[psijk[x, j, k], {j, -n, n}, {k, -2^n, 2^n -1}] /.n -> 2 // Flatten

MMA evaluates

enter image description here

Ulrich Neumann
  • 53,729
  • 2
  • 23
  • 55
  • OK! You just repeated my solution to the equation with n = 4. Can you build a solution using functions psijk[x, j, k] from @Mutaz post? – Alex Trounev May 23 '19 at 14:15
  • Add definition f[x_] := 1/ 1155 (112 (-1 + x)^(3/4) + x (144 (-1 + x)^(3/4) + x (1155 + 256 (-1 + x)^(3/4) - 1280 x^(3/4) - (1155 + 512 (-1 + x)^(3/4)) x + 1024 x^(7/4)))); – Alex Trounev May 23 '19 at 14:30
  • I'm not sure about a repetition: In my attempt there is no pointwise- discretization. Trying to understand the function psijk[x, j, k] ... – Ulrich Neumann May 23 '19 at 14:31
  • Are you kidding about the pointwise- discretization for n=3? This is a projection of the equation to get n + 1 equations for finding c[j], which is quite equivalent to your system. – Alex Trounev May 23 '19 at 15:56
  • @ Ulrich could you please provide me with a reference or link fir the Galerkin method. – Mutaz May 23 '19 at 17:57
  • Also please m, can you add another solution but by considering paijk[x,j,k] instead of g[x]? – Mutaz May 23 '19 at 18:00
  • @ Alex Trounev Sorry I'm not kidding, but needed my time to get it. You're right, the systems are equivalent. Regardless the structure of the system in my answer seems to be much more compact. – Ulrich Neumann May 23 '19 at 20:06
  • @ Mutaz For n==3 there are 112 different basisfunctions Table[ psijk[x, j, k], {j, -n, n}, {k, -2^n, 2^n - 1}] // Flatten which aren't independent. Formally you can substitude g[x]=Table[...] but you'll get a huge system. Why do you prefer these basiscfunctions? – Ulrich Neumann May 23 '19 at 20:47
  • I am using it to generalize a numerical scheme – Mutaz May 24 '19 at 09:44