hn[k_, r_] := Inactive[Sum][1/n^r, {n, 1, k}]
hn[k, r]

When Activate'd this is the HarmonicNumber
hn[k, r] // Activate
(* HarmonicNumber[k, r] *)
For your specific example
hn[k, -1/2]
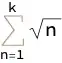
hn[k, -1/2] // Activate
(* HarmonicNumber[k, -(1/2)] *)
To see the expanded form for the first several cases
Table[hn[k, -1/2] // Activate, {k, 1, 7}]
(* {1, 1 + Sqrt[2], 1 + Sqrt[2] + Sqrt[3], 3 + Sqrt[2] + Sqrt[3],
3 + Sqrt[2] + Sqrt[3] + Sqrt[5], 3 + Sqrt[2] + Sqrt[3] + Sqrt[5] + Sqrt[6],
3 + Sqrt[2] + Sqrt[3] + Sqrt[5] + Sqrt[6] + Sqrt[7]} *)
or
Table[hn[k, -1/2], {k, 1, 7}] // Activate
(* {1, 1 + Sqrt[2], 1 + Sqrt[2] + Sqrt[3], 3 + Sqrt[2] + Sqrt[3],
3 + Sqrt[2] + Sqrt[3] + Sqrt[5], 3 + Sqrt[2] + Sqrt[3] + Sqrt[5] + Sqrt[6],
3 + Sqrt[2] + Sqrt[3] + Sqrt[5] + Sqrt[6] + Sqrt[7]} *)
If activated prior to summation, HarmonicNumber appears for higher values of k
Table[Evaluate[hn[k, -1/2] // Activate], {k, 1, 7}]
(* {1, 1 + Sqrt[2], 1 + Sqrt[2] + Sqrt[3], 3 + Sqrt[2] + Sqrt[3],
HarmonicNumber[5, -(1/2)], HarmonicNumber[6, -(1/2)],
HarmonicNumber[7, -(1/2)]} *)
FunctionExpand will convert to a sum
% // FunctionExpand
(* {1, 1 + Sqrt[2], 1 + Sqrt[2] + Sqrt[3], 3 + Sqrt[2] + Sqrt[3],
3 + Sqrt[2] + Sqrt[3] + Sqrt[5], 3 + Sqrt[2] + Sqrt[3] + Sqrt[5] + Sqrt[6],
3 + Sqrt[2] + Sqrt[3] + Sqrt[5] + Sqrt[6] + Sqrt[7]} *)

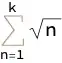
(*-HurwitzZeta[1/2, 1 + k] + Zeta[1/2]*)? – ions me May 22 '19 at 17:49
Sum[1/n,{n,1,m}]it over and over applies internal hidden rules trying to make that simpler until it doesn't change. The result isHarmonicNumber[m]. That is the simplest form it can find. Trying to force Mathematica to do other than what it usually wants can be challenging. User functions and telling to not simplify can help sometimes. – Bill May 26 '19 at 18:43