You have found one of many expressions that Mathematica, by default, does not simplify. However, it is possible to construct your own simplification functions. Here is one function for your situation:
ClearAll[tran, doit];
tran[ex_, m_: +1] :=
ex /. {Sqrt[u_ + (v_: 1) Sqrt[w_]] :> doit[u, v, w, m]};
doit[u_, v_, w_, m_: +1] := Module[{x, y, z},
x = u/v // Factor;
y = Sign[m] Sqrt[x^2 - w // Factor] // PowerExpand;
x = x + y // Factor;
z = 2 x/v // Simplify;
Sign[m] (x + Sqrt[w])/Sqrt[z] // Simplify // PowerExpand];
A simple example of usage is
3 - Sqrt[2] == tran[Sqrt[11 - 6 Sqrt[2]]]
which returns True. In your case, the usage is
ex1 = Sqrt[9 C^2 + 8 w^2 - 3 C Sqrt[9 C^2 + 16 w^2]];
ex2 = (-3 C + Sqrt[9*C^2 + 16*w^2])/Sqrt[2];
ex2 == tran[ex1]
which returns True again, as it should. The purpose of the parameter m is that sometimes the negative of the square root should be taken in the y = ... line of the doit[] code.

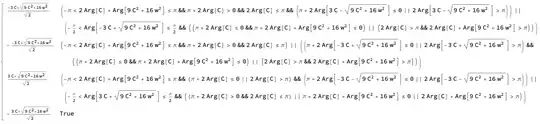
Reduce[Sqrt[ 9 c^2 + 8 w^2 - 3 c Sqrt[9 c^2 + 16 w^2]] == (-3 c + Sqrt[9*c^2 + 16*w^2])/ Sqrt[2], Reals]giveTrue. – kglr May 24 '19 at 10:10