I am trying to solve some linear, coupled PDEs for perturbative analysis (first order in time, 3rd order in space), for which I then plan to take the global spatial maxima of their magnitudes and plot them across time to show the temporal evolutions of the individual perturbations.
To solve the equations, I have attempted to use the template provided by user xzczd.
p = .011;
ky = 10;
c = 27;
Ω = 2800/p;
L = p/0.3;
v = p^2* Ω/L;
A0 = 1;
xf=3;
Θ[x_] := -(3 c (1 + p^2 ky^2)/(2 p^2*v*ky)) (Sech[
x c/(2 p*Sqrt[c^2 - ky^2 A0^2])]^2);
With[{A = A[t, x], Θ1 = Θ1[t, x],
vy = vy[t, x]},
pde1 = D[
A + p^2 (ky^2 A +
2 A0*Θ[x]*D[Θ1, x] - D[A, x, x]),
t] - c*D[
A + p^2 (ky^2 A +
2 A0*Θ[x]*D[Θ1, x] -
D[A, x, x]), x] +
p^2 (Θ[x])^2 (D[A, t] -
c*D[A, x]) == ((v p^2 ky)/(1 + (p^2 ky^2))) \
(2*(Θ[x])*D[A, x] + A0*D[Θ1, x, x]);
pde2 = A0 (D[Θ1, t] - c*D[Θ1, x]) -
p^2 (D[Θ[x], x] (D[A, t] - c*D[A, x]) +
D[A0 D[Θ1, x, x] + 2 Θ[x] D[A, x],
t] - c*D[
A0 D[Θ1, x, x] + 2 Θ[x] D[A, x],
x]) == ((v p^2 ky)/(1 + (p^2 ky^2))) (2 A0 Θ[
x] D[Θ1, x] - D[A, x, x]) -
p^2 ky A0 D[vy, x, x];
pde3 = (1/(p^4 Ω^2)) (D[vy, t] - c*D[vy, x]) ==
ky A0^2 D[Θ1, x, x] +
D[2 ky A0 A Θ[x], x];]
pde = {pde1, pde2, pde3};
ic = {A[0, x] == 10^(-5),
vy[0, x] == 0, Θ1[0, x] == 0};
bc = {A[t, xf] == 0, (D[A[t, x], x] /. x -> xf) ==
0, (D[A[t, x], x] /. x -> 0) ==
0, (D[Θ1[t, x], x] /. x -> xf) ==
0, (D[Θ1[t, x], x] /. x -> 0) ==
0, Θ1[t, xf] == 0,
vy[t, xf] == 0, (D[vy[t, x], x] /. x -> 0) == 0};
begintime = 0; endtime = 80;
points@x = 200; points@t = 25;
m = 200;
difforder = 8;
domain@x = {0, 3}; domain@t = {begintime, endtime};
(grid@# = Array[# &, points@#, domain@#]) & /@ {x, t};
ptoafunc =
pdetoae[{A, Θ1, vy}[t, x], grid /@ {t, x},
difforder];
del = #[[2 ;; -2]] &;
ae = Map[del, Most /@ ptoafunc@pde, {2}];
aeic = del /@ ptoafunc@ic;
aebc = ptoafunc@bc;
var = Outer[#[#2, #3] &, {A, Θ1, vy}, grid@t, grid@x];
{barray, marray} =
CoefficientArrays[Flatten@{ae, aeic, aebc},
Flatten@var]; // AbsoluteTiming
Block[{p = .011,
ky = 10,
c = 27,
Ω = 2800/p,
L = p/0.3,
v = p^2* Ω/L,
A0 = 1},
sollst = LinearSolve[N@marray, -barray]]; // AbsoluteTiming
solmatlst = ArrayReshape[sollst, var // Dimensions];
solfunclst = ListInterpolation[#, grid /@ {t, x}] & /@ solmatlst;
plot[f_, style_, t_] :=
Plot[solfunclst[t, x] // Through // f //
Evaluate, {x, domain@x} // Flatten // Evaluate,
PlotStyle -> style]
but I run into an error once I run the code:
{17.5364, Null}
Could someone help resolve the error in this code? Or if I should be approaching this problem through different means? I apologize for the general inexperience in this matter. Thank you very much in advance.
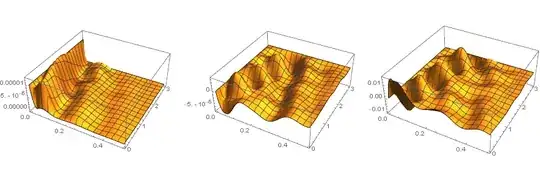
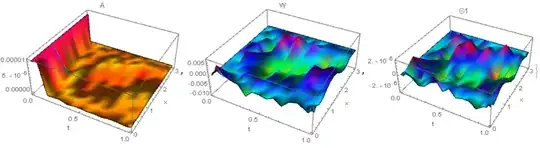
xf? – xzczd May 30 '19 at 11:01A, 1 forvy, 2 for\[CapitalTheta]1), are you sure it's enough? Usually the number of b.c. should be equal to the highest differential order in the corresponding direction for every unknown function. – xzczd May 30 '19 at 11:13ptoafunc@pde // Dimensionsandptoafunc@bc // Dimensionsand think about which part of the system should be removed. – xzczd May 30 '19 at 12:03[\[CapitalTheta]1respect toxis2rather than3, is it correct? – xzczd May 30 '19 at 12:16\[CapitalTheta]rather than\[CapitalTheta]1. – xzczd May 30 '19 at 12:23\[CapitalTheta]1[x]in your code. I suggest usingWithas shown in e.g. this answer to simplify your code so it'll be easier to check. – xzczd May 30 '19 at 12:413×25×200unknown variables to solve, while3×25×200 + 3×200 + 8×25equations at hand, you need to remove3×200 + 8×25from the system. But are you sure now the system is correct? I've tried various settings forpoints,difforder, etc., but the solution always becomes unstable very fast. – xzczd May 30 '19 at 13:09tdimension is also wrong. Now the code gives reasonable result. – xzczd May 30 '19 at 13:37