I have the following simultaneous equations.
$W=G[V](s+80)+(1-G[V])114$
$V=(1-F[W])(90-s)$
where $F$ and $G$ are cumulative distribution functions of $x$ and $y$. The variables of $x$ and $y$ are distributed according to some distribution respectively.
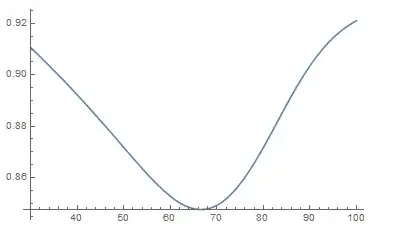
What I want to know is the minimum value of $1-F[W]$ when $s$ is changed in some range ($30<s<100$).
I solved the simultaneous equations with respect to $W$ and $V$ but was stucked when I try to find a minimum of $1-F[W]$. I could plot the graph and I could see where the minimum would be graphically.
How can I use FindMinimum or NMinimize with the solutions of the simultaneous equations? In the code below, NSolve returns a list of rules. I would like to know how I can use this list of rules to derive the minimum of $1-F[W]$.
I greatly appreciate your help.
mx = 240
dx = 100
my = 10
dy = 10
x = TruncatedDistribution[{0, ∞}, NormalDistribution[mx, dx]]
y = TruncatedDistribution[{0, ∞}, NormalDistribution[my, dy]]
f[z_] := PDF[x, z]
F[z_] := CDF[x, z]
g[z_] := PDF[y, z]
G[z_] := CDF[y, z]
sol = NSolve[{W == G[V]*(s + 80) + (1 - G[V])*114 &&
V == (1 - F[W])*(90 - s)}, {V, W}]
Plot[1 - F[W] /. sol, {s, 30, 100}]
Symbolize,SubscriptBoxand the like. – Daniel Lichtblau May 31 '19 at 18:45