How to generate all commutative pairings of list elements?

Question

Given a list with an even number of elements, e.g.

list = RandomSample[Array[e, 20]];

how can one generate a list of all different commutative pairings of the elements most efficiently in Mathematica?

A tiny example is:

list = {e[1],e[4],e[3],e[2]};
pairings[list]

{

{ {e[1],e[2]} , {e[3],e[4]} } ,

{ {e[1],e[3]} , {e[2],e[4]} } ,

{ {e[1],e[4]} , {e[2],e[3]} } ,

}

Note how the commutativity of the pairings sets e.g. {e[1],e[2]} and {e[2],e[1]} to be the same pair, so that only one such term is generated.

EDIT:

Alternatively, one can ask this question in terms of graphs:

How to generate all distinct sets of disconnected un-directed edges from a list of vertices most efficiently?

@ChristopherLamb This creates a list of all possible pairs. But starting with a list of 2n elements, we are looking for a list of groups of n pairs instead. — Kagaratsch, Jun 03 '19 at 21:12
DeleteDuplicates@Partitions[Permutation[{LIST}],2] (* More or less if a function name is wrong you could check the documentation center *) — Schopenhauer, Jun 04 '19 at 00:15
@Schopenhauer That would certainly work. However, Permutation generates n! terms, while the symmetry of the pairings actually reduces the problem to generating only (n-1)!! terms. Which is way fewer, so that the recursive functions in the answers are guaranteed to be more efficient. — Kagaratsch, Jun 04 '19 at 00:18
@Schopenhauer Assuming that each permutation only takes up 1 byte (which is too optimistic of course), note that e.g. for size 20 we have (20-1)!! == 654 729 075 (so around 600mb of data), while 20! == 2432902008176640000 (so around 2432902 terabytes of data). Unfortunately, I don't have a spare 2432902 terabyte drive lying around, hahaha! ^^ — Kagaratsch, Jun 04 '19 at 00:28
@Kagaratsch In that case you could try to narrow down the property or pattern you are trying to study on the whiteboard first. I usually try a smaller version of the problem or a geometric, modular, statistical or graph theoretical version on the small side and try to poke it to get a much simpler version and it usually work. Although I love the language the only problem with a recursive function call in Mathematica is that to process a large amount of data a Trace call to debug would be as big as the initial problem. — Schopenhauer, Jun 04 '19 at 00:39
@Schopenhauer True, definitely have to iron out all the bugs on smaller sized examples first, before running it over night on the big one. — Kagaratsch, Jun 04 '19 at 00:43
@Kagaratsch partition[l_, v_, comp_] := Flatten /@ Reap [ Scan [ Which[ comp[ v, #], Sow[#, -1], comp[v, #], Sow[#, 1], True, Sow[#,0]]&,l], {-1,0,1}][[2]] (* Three way partition function using and ordering function by sowing values with tags -1,0, or 1, depending on a relation. You could build up a list by specifying tags with Sow and patterns that match those tags in Reap. If you build the list piece by piece with recursion I would not recommend using Append instead an approach using Reap and Sow could be more effective to collect intermediate results*) — Schopenhauer, Jun 04 '19 at 01:55
@Kagaratsch I’ve seen programs that use Fold as alternative to recursion. g[{}] = x; g[l_] = f[First[l], g[Rest[l]]; could be translated to g[l_]= Fold[f[#1,#2]&, x,l]. — Schopenhauer, Jun 04 '19 at 02:08
@Kagaratsch I would also check the ??Developer`* and ??Experimental`* contexts for hidden gems like PartitionMap. — Schopenhauer, Jun 04 '19 at 02:14
@Schopenhauer Wow, thanks! Those are very useful tips and ideas! — Kagaratsch, Jun 04 '19 at 02:28

score 4 · Accepted Answer · answered Jun 03 '19 at 21:48

I think the number of such pairings is given by:

pairCounts[n_?EvenQ] := Multinomial @@ ConstantArray[2, n/2]/(n/2)!

So, you will get:

pairCounts[20]

654729075

which is a lot of pairings for a list of length 20. What do you plan to do with this list?

At any rate, here is a not very efficient method:

partitions[{a_,b_}] := {{{a,b}}}
partitions[{a_,b__}] := Catenate@Table[
    Prepend[{a, {b}[[i]]}] /@ partitions[Delete[{b}, i]],
    {i, Length[{b}]}
]

For example:

partitions[Range[4]]
partitions[Range[6]]

{{{1, 2}, {3, 4}}, {{1, 3}, {2, 4}}, {{1, 4}, {2, 3}}}

{{{1, 2}, {3, 4}, {5, 6}}, {{1, 2}, {3, 5}, {4, 6}}, {{1, 2}, {3, 6}, {4, 5}}, {{1, 3}, {2, 4}, {5, 6}}, {{1, 3}, {2, 5}, {4, 6}}, {{1, 3}, {2, 6}, {4, 5}}, {{1, 4}, {2, 3}, {5, 6}}, {{1, 4}, {2, 5}, {3, 6}}, {{1, 4}, {2, 6}, {3, 5}}, {{1, 5}, {2, 3}, {4, 6}}, {{1, 5}, {2, 4}, {3, 6}}, {{1, 5}, {2, 6}, {3, 4}}, {{1, 6}, {2, 3}, {4, 5}}, {{1, 6}, {2, 4}, {3, 5}}, {{1, 6}, {2, 5}, {3, 4}}}

Thanks, this one is quicker than the one I could write! I plan to collapse some of the vertices to obtain connected graphs and determine their multiplicity. — Kagaratsch, Jun 03 '19 at 22:16

kglr · Answer 2 · 2019-06-04T07:52:00.267

ClearAll[perfectMatchings]
perfectMatchings = Module[{subs = Subsets[#, {2}], l = Length @ #, matchings},
    matchings = FindIndependentVertexSet[LineGraph[UndirectedEdge @@@ subs], l/2, All];
    Extract[subs, List /@ matchings] ] &;

perfectMatchings[Range @ 4] // Grid // TeXForm

$\small\begin{array}{cc} \{1,4\} & \{2,3\} \\ \{1,3\} & \{2,4\} \\ \{1,2\} & \{3,4\} \\ \end{array}$

perfectMatchings[Range @ 6] // Grid // TeXForm

$\small\begin{array}{ccc} \{1,6\} & \{2,5\} & \{3,4\} \\ \{1,6\} & \{2,4\} & \{3,5\} \\ \{1,6\} & \{2,3\} & \{4,5\} \\ \{1,5\} & \{2,6\} & \{3,4\} \\ \{1,5\} & \{2,4\} & \{3,6\} \\ \{1,5\} & \{2,3\} & \{4,6\} \\ \{1,4\} & \{2,6\} & \{3,5\} \\ \{1,4\} & \{2,5\} & \{3,6\} \\ \{1,4\} & \{2,3\} & \{5,6\} \\ \{1,3\} & \{2,6\} & \{4,5\} \\ \{1,3\} & \{2,5\} & \{4,6\} \\ \{1,3\} & \{2,4\} & \{5,6\} \\ \{1,2\} & \{3,6\} & \{4,5\} \\ \{1,2\} & \{3,5\} & \{4,6\} \\ \{1,2\} & \{3,4\} & \{5,6\} \\ \end{array}$

Note: This is much slower than Carl's partitions and Kagaratsch's pairings.

Kagaratsch · Answer 3 · 2019-06-03T22:41:19.437

Here a recursive solution, which I suspect is similar to the one by Carl Woll:

pairings[list_, progress_] := Block[{},
  If[Length[list] > 1,
   Flatten[
    Table[
     pairings[Drop[list[[2 ;;]], {i - 1}], 
      Append[progress, {list[[1]], list[[i]]}]]
     , {i, 2, Length[list]}]
    , 1]
   ,
   p[progress]
   ]
  ]

With outputs

pairings[Range[4], {}]

{p[{{1, 2}, {3, 4}}], p[{{1, 3}, {2, 4}}], p[{{1, 4}, {2, 3}}]}

and

pairings[Range[6], {}]

{p[{{1, 2}, {3, 4}, {5, 6}}], p[{{1, 2}, {3, 5}, {4, 6}}],

p[{{1, 2}, {3, 6}, {4, 5}}], p[{{1, 3}, {2, 4}, {5, 6}}],

p[{{1, 3}, {2, 5}, {4, 6}}], p[{{1, 3}, {2, 6}, {4, 5}}],

p[{{1, 4}, {2, 3}, {5, 6}}], p[{{1, 4}, {2, 5}, {3, 6}}],

p[{{1, 4}, {2, 6}, {3, 5}}], p[{{1, 5}, {2, 3}, {4, 6}}],

p[{{1, 5}, {2, 4}, {3, 6}}], p[{{1, 5}, {2, 6}, {3, 4}}],

p[{{1, 6}, {2, 3}, {4, 5}}], p[{{1, 6}, {2, 4}, {3, 5}}],

p[{{1, 6}, {2, 5}, {3, 4}}]}

Turns out, this one is a bit slower than partitions by Carl Woll:

pairings[Range[14], {}] // Length // AbsoluteTiming

{1.91637, 135135}

partitions[Range[14]] // Length // AbsoluteTiming

{1.1277, 135135}

Anjan Kumar · Answer 4 · 2019-06-04T13:48:30.567

This question kind of looks similar to 167488 IMO.

The answer here uses the same idea of the answer.

commPairs[list_] := Module[{perms},
   perms = 
    Table[(ConstantArray[Unique[], {2}]), Length[list]/2] // Flatten //
      Permutations;
   Keys@GatherBy[#, Last] & /@ (Thread[list -> #] & /@ perms) // 
    DeleteDuplicates
   ];

Test:

commPairs[Range@4]

{{{1, 2}, {3, 4}}, {{1, 3}, {2, 4}}, {{1, 4}, {2, 3}}}

commPairs[Range@6]

{{{1, 2}, {3, 4}, {5, 6}}, {{1, 2}, {3, 5}, {4, 6}}, {{1, 2}, {3, 6}, {4, 5}}, {{1, 3}, {2, 4}, {5, 6}}, {{1, 3}, {2, 5}, {4, 6}}, {{1, 3}, {2, 6}, {4, 5}}, {{1, 4}, {2, 3}, {5, 6}}, {{1, 5}, {2, 3}, {4, 6}}, {{1, 6}, {2, 3}, {4, 5}}, {{1, 4}, {2, 5}, {3, 6}}, {{1, 4}, {2, 6}, {3, 5}}, {{1, 5}, {2, 4}, {3, 6}}, {{1, 6}, {2, 4}, {3, 5}}, {{1, 5}, {2, 6}, {3, 4}}, {{1, 6}, {2, 5}, {3, 4}}}

Unfortunately, generating all n! permutations in the intermediate terms instead of just the (n-1)!! needed ones makes this kind of slow. — Kagaratsch, Jun 06 '19 at 18:58

JEM_Mosig · Answer 5 · 2022-05-02T12:44:59.700

Here is one more recursive answer that I find slightly easier to read:

ClearAll[jemPairings];
jemPairings[list_?VectorQ] := Catch@Module[
    {two, rest, restpairings, pivot},
If[Length[list] == 2, Throw[{{list}}]];

{two, rest} = TakeDrop[list, 2];
restpairings = jemPairings[rest];
pivot = two[[2]];

Table[
 Splice@Table[
   {two /. pivot -&gt; j, Splice[Sort /@ (rest /. j -&gt; pivot)]},
   {rest, restpairings}
   ],
 (* Let j be every remaining item (including pivot) *)
 {j, Union@Flatten[{pivot, restpairings}]}
 ]
] /; EvenQ@Length[list] &amp;&amp; Length[list] &gt;= 2

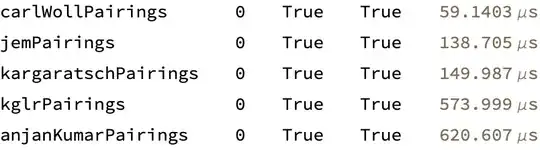
The Sort /@ is not really necessary, but nice to have. It's the second fastest so far (Mathematica 13.0.1 on MacBook Pro):

TableForm@SortBy[
  Table[
   {
    f,
    Length[ReleaseHold[f[Range[8]] /. p -> Identity]] - (8 - 1)!!,
    ReleaseHold[f[Range[2]]] == {{{1, 2}}} /. p -> Identity,
    Sort[
       Sort /@ 
        ReleaseHold[f[Range[6]]]] == {{{1, 2}, {3, 4}, {5, 6}}, {{1, 
         2}, {3, 5}, {4, 6}}, {{1, 2}, {3, 6}, {4, 5}}, {{1, 3}, {2, 
         4}, {5, 6}}, {{1, 3}, {2, 5}, {4, 6}}, {{1, 3}, {2, 6}, {4, 
         5}}, {{1, 4}, {2, 3}, {5, 6}}, {{1, 4}, {2, 5}, {3, 6}}, {{1,
          4}, {2, 6}, {3, 5}}, {{1, 5}, {2, 3}, {4, 6}}, {{1, 5}, {2, 
         4}, {3, 6}}, {{1, 5}, {2, 6}, {3, 4}}, {{1, 6}, {2, 3}, {4, 
         5}}, {{1, 6}, {2, 4}, {3, 5}}, {{1, 6}, {2, 5}, {3, 4}}} /. 
     p -> Identity,
    UnitConvert[
     Quantity[First@RepeatedTiming[ReleaseHold[f[Range[6]]]], 
      "Seconds"], "Microseconds"]
    },
   {f, {jemPairings, carlWollPairings, anjanKumarPairings, 
     HoldForm@kglrPairings, kargaratschPairings}}
   ],
  Last
  ]

score 0 · Answer 6 · answered Jun 03 '19 at 21:26

0

How is it that the comment by @ChristopherLamb is incorrect? Sets are order independent, so I would think this creates "commutative pairs."

set = Table[e[n], {n, 4}]

(* {e[1],e[2],e[3],e[4]} *)

Subsets[set, {2}]

(* {{e[1],e[2]},{e[1],e[3]},{e[1],e[4]},{e[2],e[3]},{e[2],e[4]},{e[3],e[4]}} *)

answered Jun 03 '19 at 21:26

David Keith

4,340
1
12
28

This output is missing a dimension in the list, which would partition this set of pairs into groups of pairs in which all elements show up exactly once. Also note that some edges will exist more than once within these groups when list dimension is larger than 4. – Kagaratsch Jun 03 '19 at 21:39

How to generate all commutative pairings of list elements?

6 Answers6