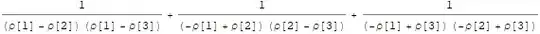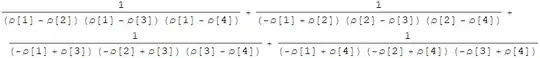1

I have the following term which I would like to express correctly in Mathematica:

$$\sum_{i=1}^{m}\frac{1}{\prod_{j=1,j\neq i}^m(\rho_i-\rho_j)}$$

This means that for $m=3$ for example you should get the following

$$ \frac{1}{(\rho_1-\rho_2)(\rho_1-\rho_3)}+\frac{1}{(\rho_2-\rho_1)(\rho_2-\rho_3)}+\frac{1}{(\rho_3-\rho_2)(\rho_3-\rho_1)} $$

Can you please help?

user64494
  • 26,149
  • 4
  • 27
  • 56
Y.L
  • 181
  • 3
  • There is no duplication since the other question does not have a sum and thus the $i$ is not well defined. I chose to put a new question instead of creating some confusion. – Y.L Jun 05 '19 at 14:44

3 Answers3

2
With[{m = 3},
  Sum[1/Product[ρ[i] - ρ[j], {j, DeleteCases[Range[m], i]}], {i, m}]]

$$ \frac{1}{(\rho (2)-\rho (1)) (\rho (2)-\rho (3))}+\frac{1}{(\rho (3)-\rho (1)) (\rho (3)-\rho (2))}+\frac{1}{(\rho (1)-\rho (2)) (\rho (1)-\rho (3))} $$

Here I used ρ[i] instead of Subscript[ρ,i] because subscripts are a pitfall for new users.

Update: It's easier to use Drop instead of DeleteCases, as in @kglr's solution:

With[{m = 3}, 
  Sum[1/Product[ρ[i] - ρ[j], {j, Drop[Range[m], {i}]}], {i, m}]]
Roman
  • 47,322
  • 2
  • 55
  • 121
1
f[m_Integer] := Sum[1/Product[(Subscript[\[Rho], i] - Subscript[\[Rho], j]),
    {j, Complement[Range[1, m], {i}]}], {i, m}]

f[3]

enter image description here

Chris Degnen
  • 30,927
  • 2
  • 54
  • 108
0
ClearAll[f1, f2]
f1[m_] := Module[{a = Array[ρ, m]}, m / 
  HarmonicMean @ MapIndexed[Apply[Times] @* Drop, Outer[Subtract, a, a]]

f2[m_] := Module[{a = Array[ρ, m]}, 
  m Moment[ MapIndexed[Apply[Times] @* Drop, Outer[Subtract, a, a], -1]]


f1[3]

enter image description here

f1[4]

enter image description here

And @@ (f1[#] == f2[#] & /@ Range[100])

True

kglr
  • 394,356
  • 18
  • 477
  • 896