5

I am trying to create products following an anti-commutative rules using the binary operator **. I define my rules the following way:

before___ ** a_ ** b_ ** after___ :>  
  If[OrderedQ[{a, b}] == True,
    before ** a ** b ** after,
    before ** ((-1)*b) ** a ** after],
NonCommutativeMultiply[x_] :> x

This does half the job that I want, since it transforms the following expression

$$o_{1,2}\text{**}o_{1,3}\text{**}o_{2,3}-o_{1,2}\text{**}o_{2,3}\text{**}o_{1,3}-o_{1,3}\text{**}o_{1,2}\text{**}o_{2,3}+o_{1,3}\text{**}o_{2,3}\text{**}o_{1,2}+o_{2,3}\text{**}o_{1,2}\text{**}o_{1,3}-o_{2,3}\text{**}o_{1,3}\text{**}o_{1,2}$$

into

$$2 o_{1,2}\text{**}o_{1,3}\text{**}o_{2,3}-2 o_{1,2}\text{**}o_{2,3}\text{**}o_{1,3}+2 o_{1,3}\text{**}o_{2,3}\text{**}o_{1,2}$$

I ultimately want to reduce the expression to

$$ 6 o_{1,2}\text{**}o_{1,3}\text{**}o_{2,3}$$

(Please add the appropriate tags for this question as I didn't find anything I deem suitable).

Kagaratsch
  • 11,955
  • 4
  • 25
  • 72
Alonso Perez-Lona
  • 281
  • 1
  • 6

1 Answers1

7

I suggest using CenterDot wrapper for the multiplication symbol instead of NonCommutativeMultiply. The former, just as the latter, does not commute terms by default, but it also has no pre-defined properties in Mathematica, which makes it easy to assign new properties to it:

ClearAll[CenterDot]
CenterDot[x___, CenterDot[y___], z___] := CenterDot[x, y, z]
CenterDot[x___, q_ CenterDot[y___], z___] :=q CenterDot[x, y, z]
CenterDot[x___, Times[-1, CenterDot[y___]], z___] :=- CenterDot[x, y, z]
CenterDot[x___, y_ + z_, q___] := CenterDot[x, y, q] + CenterDot[x, z, q]
CenterDot[x___, y_ Subscript[o_, a_, b_], z___] := y CenterDot[x, Subscript[o, a, b], z]
CenterDot[x___, Times[-1, Subscript[o_, a_, b_]], z___] := - CenterDot[x, Subscript[o, a, b], z]
CenterDot[x___,y_,z___]/;FreeQ[y,Subscript[o_, a_, b_]]:=y CenterDot[x,z]
CenterDot[x_]:=x
CenterDot[]:=1
CenterDot[x___] /; ! OrderedQ[{x}] := Signature[{x}] CenterDot[Sort[{x}] /. List -> Sequence]

This directly leads to

Subscript[o, 1, 2] \[CenterDot] Subscript[o, 1, 3] \[CenterDot] Subscript[o, 2, 3] - Subscript[o, 1, 2] \[CenterDot] Subscript[o, 2, 3] \[CenterDot] Subscript[o, 1, 3] - 
Subscript[o, 1, 3] \[CenterDot] Subscript[o, 1, 2] \[CenterDot] Subscript[o, 2, 3] + Subscript[o, 1, 3] \[CenterDot] Subscript[o, 2, 3] \[CenterDot] Subscript[o, 1, 2] + 
Subscript[o, 2, 3] \[CenterDot] Subscript[o, 1, 2] \[CenterDot] Subscript[o, 1, 3] - Subscript[o, 2, 3] \[CenterDot] Subscript[o, 1, 3] \[CenterDot] Subscript[o, 1, 2]

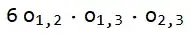
enter image description here

Kagaratsch
  • 11,955
  • 4
  • 25
  • 72
  • Hello. What new rule should I set if I get things like 1 \[CentralDot] Subscript[o,a,b] - Subscript[o,a,b] and -(1 \[CentralDot] Subscript[o,a,b]) + Subscript[o,a,b] ? – Alonso Perez-Lona Jun 07 '19 at 12:33
  • @AlonsoPerezLona added three more rules that should do this. – Kagaratsch Jun 07 '19 at 13:13
  • That is great, thank you! – Alonso Perez-Lona Jun 07 '19 at 13:24
  • I have another problem now. I had the expression (-3*1 \[CenterDot] (-Subscript[t, 1, 2]) \[CenterDot] Subscript[t, 1, 3] \[CenterDot] (-Subscript[t, 2, 3]) + 3*1 \[CenterDot] Subscript[t, 1, 2] \[CenterDot] (-Subscript[t, 1, 3]) \[CenterDot] Subscript[t, 2, 3])/(24*Pi^2)

    with the previous set of rules. Now with these rules this term goes to 0 instead of 6 the expression

     – Alonso Perez-Lona Jun 07 '19 at 13:44
  • @AlonsoPerezLona a really important subtlety is that the rules treat only quantities that look like Subscript[o,_,_] as operators, while everything else is treated as a constant. So the Subscript[t,_,_] quantities are treated as constants. If you need both, Subscript[o,_,_] AND Subscript[t,_,_] to be treated as operators, you could make the pattern look like Subscript[_,_,_] -- so any symbol with two subscripts would be anticommuting with any other symbol that fits this description. Is that what you want to do? – Kagaratsch Jun 07 '19 at 14:03
  • That's correct. – Alonso Perez-Lona Jun 07 '19 at 14:07
  • @AlonsoPerezLona Try the updated rules (make sure all appear in the current order). This implements the anti-commutator algebra ${A_{i,j},B_{k,l}}=0$ where $A$ and $B$ are arbitrary operator names that are either the same or different. – Kagaratsch Jun 07 '19 at 14:18
  • 1
    Awesome, thank you very much. – Alonso Perez-Lona Jun 07 '19 at 15:23