Collecting terms from expression with indexed functions

Question

Say I have an expansion of terms containing functions y[j,t] and its derivatives, indexed by j with the index beginning at 0 whose independent variable are t, like so:

Expr = y[0,t]^2 + D[y[0,t],t]*y[0,t] + y[0,t]*y[1,t] + y[0,t]*D[y[1,t],t] + (y[1,t])^2*y[0,t] + ... etc.

Now I wish to define new functions indexed by i, call them A[i], that collect all terms from the expression above such that the sum of the indices of the factors in each term sums to i.

In the above case for the terms shown we would have for example

A[0] = y[0,t]^2 + D[y[0,t],t]*y[0,t]

A[1] = y[0,t]*y[1,t] + y[0,t]*D[y[1,t],t]

A[2] = (y[1,t])^2*y[0,t]

How can I get mathematica to assign these terms to these new functions automatically for all i?

Note: If there is a better way to be indexing functions also feel free to suggest.

Kagaratsch · Accepted Answer · 2019-06-06T19:14:19.410

2

You can get the result in a list form for example as follows:

Reverse[MonomialList[Expr /. y[x_, z_] -> EPS^x*y[x, z] /. Derivative[A_, B_][y][x_, z_] -> EPS^x*Derivative[A, B][y][x, z], EPS]] /. EPS -> 1

This replaces all instances of y or its derivatives by EPS to the power of first argument of the original y times itself. Then one can collect different monomials in EPS to a list and set the EPS back to 1 at the end.

edited Jun 06 '19 at 19:14

answered Jun 06 '19 at 19:06

Kagaratsch

11,955
4
25
72

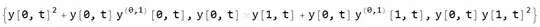
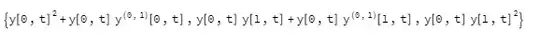
I have a problem now, when I later on define y[0,t] say as y[0,t_] = 1+2t and then I recall the above elements of the list, the derivative Derivative[0, 1][y][0, t] will not evaluate with the new definition, it is left in its general form. How can I ensure that they are evaluated once the element of the list is called after I have defined y[0,t]? – Decebalus Jul 10 '19 at 20:48
@Decebalus if you define y to be an explicit function, this will break the routine that sorts the terms. I suggest, instead of locking in a definition, to use a substitution instead, whenever needed: /. y :> (If[#1 === 0, 1 + 2 #2, y[#1, #2]] &) -- This substitutes a function for each y where #2 is the second argument of this function whenever the first argument #1 is equal to 0. – Kagaratsch Jul 10 '19 at 21:33
Thanks I will think about this, in the meantime would you mind having a look at this? link – Decebalus Jul 10 '19 at 21:51

score 2 · Answer 2 · answered Jun 07 '19 at 08:15

You can also use Cases to construct a function that computes the index-sum and use it with GatherBy to group the monomials:

ClearAll[f0, f1]
f0 = Total @* Cases[(y | Derivative[__][y])[i_, _]^p_. :> p i];
f1 = Total /@ GatherBy[SortBy[f0]@MonomialList[#], f0]&;

f1 @ Expr

Collecting terms from expression with indexed functions

2 Answers2