I am trying to find the first three lowest eigenvalues of large sparse matrices of size range $10^3 - 10^5$. The matrices depend on some parameter $x$, so I first construct the matrices and then use Eigenvalues[Mat(x), 3]. Mathematica however orders the eigenvalues by absolute value so there is no guarantee in finding the lowest eigenvalue by the method above. See figure below
I can find all the eigenvalues, order them, and then find the minimum using the instructions found here but that defeats the point of using sparse matrices or Mathematica altogether. Moreover, the code slows down even more when cycling through all values of $x$. So, can this problem be done in Mathematica?
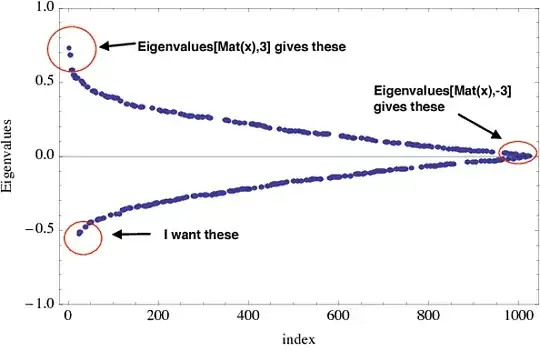
Eigenvalues[Mat[x], -3]? – Carl Woll Jun 10 '19 at 17:58m[x]of low dimension. – Alex Trounev Jun 10 '19 at 18:05