Find surrounding vertices (simplexes) of a given point for DelaunayMesh

Question

Generating a Delaunay triangulation of some random points:

pts = RandomReal[{-1, 1}, {50, 2}];
dm = DelaunayMesh[pts];
HighlightMesh[dm, Style[0, Black]]

gives

[

For a point e.g. {0.3, 0.24}

How do I get the element this falls in, i.e. the three surrounding vertices/simplexes (in Python, in the spicy.spatial.Delaunay module, this would be the find_simplex command)?

Answer 1

You can use the property "VertexVertexConnectivityRules" to create an association and use it to find the indices of neighboring vertices:

ClearAll[neighboringPoints]
neighboringPoints = Association @ dm["VertexVertexConnectivityRules"];
HighlightMesh[dm, {Style[0, Black], 
  Style[{0, 1}, Directive[Green, PointSize[Large]]], 
  Style[{0, #} & /@ neighboringPoints[1], Directive[Red, PointSize[Large]]]}]

neighboringPoints takes an index(i) and returns the indices of neighbors of pts[i]:

neighboringPoints[5]

{42, 32, 49, 8, 38}

You can use it to define a function that takes a list of coordinates and returns the list of neighboring coordinates:

neighboringCoords[p_] := p[[neighboringPoints @ (First@PositionIndex[p][#])]] &;
pts[[5]]

{0.101634, -0.362799}

neighboringCoords[pts] @ {0.101634, -0.362799}

{{-0.0193242, -0.316663}, {-0.041939, -0.584718}, {0.369882, -0.553096}, {0.727515, -0.244872}, {0.202586, 0.17428}}

Similarly, you can use the properties "VertexEdgeConnectivityRules" and "VertexFaceConnectivityRules" to find the indices of neighboring edges and faces, respectively:

ClearAll[neighboringEdges, neighboringFaces]
neighboringEdges = Association@dm["VertexEdgeConnectivityRules"];
neighboringFaces = Association@dm["VertexFaceConnectivityRules"];


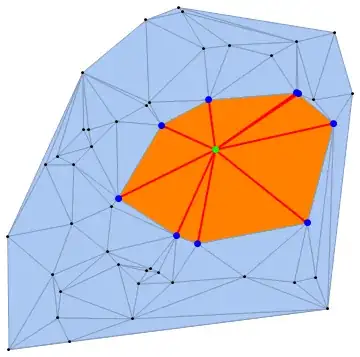
k = 38;
HighlightMesh[dm, {Style[0, Black], 
  Style[{0, k}, Directive[Green, PointSize[Large]]],
  Style[{0, #} & /@ neighboringPoints[k], Directive[Blue, PointSize[Large]]],
  Style[{2, #} & /@ neighboringFaces[k], Orange], 
  Style[{1, #} & /@ neighboringEdges[k], Directive[Red, Thick]]}]

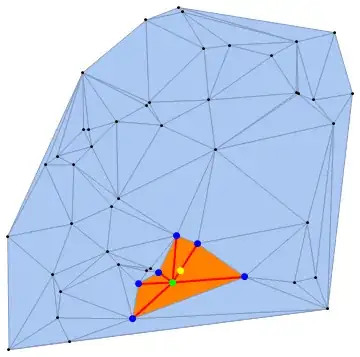
We can also use a random point (rp) inside the convex hull of pts as input, find the vertex closest to rp and show its neighboring vertices, edges and faces:

nF = Nearest[pts -> "Index"];
SeedRandom[7777]
rp = RandomPoint[ConvexHullMesh @ pts];
k = First @ nF[rp];
HighlightMesh[dm, {Style[0, Black], 
  Style[{0, k}, Directive[Green, PointSize[Large]]],
  Style[{0, #} & /@ neighboringPoints[k], Directive[Blue, PointSize[Large]]],
  Style[{2, #} & /@ neighboringFaces[k], Orange], 
  Style[{1, #} & /@ neighboringEdges[k], Directive[Red, Thick]]}, 
 Epilog -> {PointSize[Large], Yellow, Point@rp}]