0

I have an example from Stewart's Calculus where the equation $y'' + y = 0$ is solved using power series. The equation 

Subscript[c, 2 + n] == -(Subscript[c, n]/((n + 1) (n + 2)))

is used to determine the coefficients recursively and is straightforward to solve "by hand", but I cannot see how to do this in Mathematica. Searching for "Recursion Relation" in the Wolfram Language & System Documentation Center returns a tutorial Functions That Remember Values They Have Found, which uses the example of a Fibonacci function

f[x_] := f[x] = f[x - 1] + f[x - 2]

with conditions 

f[0] = f[1] = 1

I have followed this example to input a function to calculate the coefficients recursively, but whatever I try I get a $RecursionLimit error. I would be grateful if someone could explain how to enter such a function since I am clearly misunderstanding the basic concept behind this in some way.

m_goldberg
  • 107,779
  • 16
  • 103
  • 257
BenNevis
  • 3
  • 2
  • Welcome to Mathematica.SE! I suggest the following: 1) As you receive help, try to give it too, by answering questions in your area of expertise. 2) Take the tour! 3) When you see good questions and answers, vote them up by clicking the gray triangles, because the credibility of the system is based on the reputation gained by users sharing their knowledge. Also, please remember to accept the answer, if any, that solves your problem, by clicking the checkmark sign! – Michael E2 Jun 20 '19 at 19:52
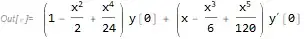
  • You can format inline code and code blocks by selecting the code and clicking the {} button above the edit window. The edit window help button ? is useful for learning how to format your questions and answers. You may also find this meta Q&A helpful – Michael E2 Jun 20 '19 at 19:52
  • Related: https://mathematica.stackexchange.com/questions/25363/solving-an-ode-in-power-series – Michael E2 Jun 20 '19 at 19:55

2 Answers2

1

y'' + y = 0 is solved using power series

Is this what you are looking for?

ClearAll[y,x];
ode = y''[x] + y[x] == 0;
sol = AsymptoticDSolveValue[ode, y[x], {x, 0, 5}];
sol /. {C[1] -> y[0], C[2] -> y'[0]}

Mathematica graphics

Nasser
  • 143,286
  • 11
  • 154
  • 359
  • @BenNevis This is a new function. I looked docs now, and it said it was added in 11.3 – Nasser Jun 20 '19 at 17:40
  • @BenNevis You need to have your ODE in there. I'll add it now. Mathematica will not show you the steps of how it obtained the series solution like the text book does. For this you need step-by-step solver. I do not know any one which will show all the steps like in the textbook. I do not think Wolfram Alpha pro even shows these steps but you could try it. – Nasser Jun 20 '19 at 17:41
0

One way is to use the provided function for solving recurrences. The following example code

sol = c[n] /. RSolve[ {c[n + 2] == 
   -c[n]/((n + 1) (n + 2)),
   c[0] == c0, c[1] == c1}, c[n], n][[1, 1]];
sol /. n -> # & /@ Range[0, 5] // InputForm

returns the result

{c0, c1, -c0/2, -c1/6, c0/24, c1/120}

as expected. Another way is to define a recursive function. The example code

ClearAll[c];
c[0] = c0; c[1] = c1;
c[m_] := c[m] = With[{n = m - 2},
   -c[n]/((n + 1) (n + 2))];
c /@ Range[0, 5] // InputForm

returns the same result as the previous example. Notice the memoization c[m_]:=c[m]= as well as the ClearAll[c].

Somos
  • 4,897
  • 1
  • 9
  • 15