Plotting with Precision

Question

Suppose we plot

Plot[Exp[x] Exp[-x], {x, 0, 1000}]

This equals $1$, as expected, until around $x = 750$ where the curve drops sharply to $0$. Clearly this is due to precision / accuracy issues. How do you fix this plot?

The obvious algebraic simplification here is not the point, as my actual example is closer to:

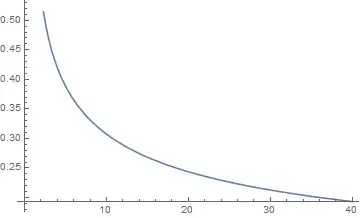
Plot[Exp[-x^2] Hypergeometric1F1[1/3, 1/2, x^2], {x, 0, 40}]

which fails around $x = 27$, where it drops abruptly to $0$. The Exp and Hypergeometric1F1 terms respectively shrink and grow extremely rapidly, but nearly cancel one another, so their product should remain close to $1$.

OK, could it be a version and/or platform specific problem then? I am using Mathematica v11.3.0.0 on 64 bit Windows 10 — Colin MacLaurin, Jun 27 '19 at 13:09
@UlrichNeumann The change happened in V11.3. See (170416)/(56728) — Michael E2, Jun 28 '19 at 00:55

score 7 · Accepted Answer · answered Jun 27 '19 at 13:24

7

Use the Plot option Evaluated

Plot[Exp[x] Exp[-x], {x, 0, 1000}, Evaluated -> True]

Or Evaluate the argument

Plot[Evaluate[Exp[x] Exp[-x]], {x, 0, 1000}]

Or use arbitrary-precision rather than machine precision.

Plot[Exp[x] Exp[-x], {x, 0, 1000}, WorkingPrecision -> 20]

answered Jun 27 '19 at 13:24

Bob Hanlon

157,611
7
77
198

These all work on my machine. The last answer also works on my real example, with the hypergeometric function. Thank-you! – Colin MacLaurin Jun 27 '19 at 13:44

score 3 · Answer 2 · answered May 13 '20 at 11:23

The Exp and Hypergeometric terms respectively shrink and grow extremely rapidly, but nearly cancel one another, so their product should remain close to 1.

The right way to cure the cancellation problem of the OP is to use the Kummer transformation:

Exp[-x^2] Hypergeometric1F1[1/3, 1/2, x^2] /. 
Hypergeometric1F1[a_, b_, z_] :> Exp[z] Hypergeometric1F1[b - a, b, -z]
   Hypergeometric1F1[1/6, 1/2, -x^2]

which results in a function that is more numerically agreeable:

Plot[Hypergeometric1F1[1/6, 1/2, -x^2], {x, 0, 40}]

plot of Kummer function

score 2 · Answer 3 · answered Jun 27 '19 at 12:34

2

I found a solution using a separate function, with an intermediate variable y:

myfunc[x_] := Module[ {y}, y=SetPrecision[x,20]; Exp[-y^2]Hypergeometric1F1[1/3,1/2,y^2] ]

Plot[ myfunc[x], {x,0,40}, PlotRange->{0,1} ]

Now the plot is smooth. Maybe this answer will be helpful to someone. It also seems inelegant, so perhaps there is a better solution.

answered Jun 27 '19 at 12:34

Colin MacLaurin

155
6

You might want myfunc[x_?MachineNumberQ] := myfunc[SetPrecision[x, 20]; myfunc[x_?NumericQ] := Exp[-x^2] Hypergeometric1F1[1/3,1/2,x^2]; -- not sure about the ?NumericQ. It depends on whether you want myfunc[z] to evaluate to the symbolic expression, at which point you lose control of the precision. – Michael E2 Jun 28 '19 at 00:50

Plotting with Precision

3 Answers3