6

This post is not about a specific Mathematica problem but about to develop the best way to enter mathematical equations with subscripts and superscripts. I have a model of a large number of equations in which variables have subscripts, superscripts, and an index to create a set of equations using Table.

I wonder if anybody can suggest me the best way to enter model equations such as those in dynamic stochastic equilibrium models. Equations have all kinds of subscripts and superscripts, and I like to know the best way of writing such equations in Mathematica.

EDIT 1 Here is an example of a model I aim to solve. Using the suggested subscript and superscript notation to write a Mathematica code will be very complicated and there must be another way to code this model because Mathematica is supposed to be powerful solve much more complicated and larger system of non-linear equations.

enter image description here enter image description here

As can be easily seen from this example model, I could log-linearize the model and redefine the variables and solve the system. My question is not about solving this model but entering the model equations in an efficient format using Mathematica. It is obvious to me that using long-subscript and superscripted variables is not the way forward. I am interested in a robust and stable coding of model of this kind.

I hope my question is clear.

Thanks.

Tugrul Temel
  • 6,193
  • 3
  • 12
  • 32
  • 3
    There are some limitations that you can face when using sub/super-scripts https://mathematica.stackexchange.com/questions/1004/can-we-use-letter-with-a-subscript-as-a-variable-in-mathematica – yarchik Jun 30 '19 at 07:53
  • 3
    For instance, you cannot clear a value of such an object easily https://mathematica.stackexchange.com/questions/373/clear-complains-that-a-subscripted-variable-is-not-a-symbol-or-a-string?noredirect=1&lq=1 – yarchik Jun 30 '19 at 07:54
  • 12
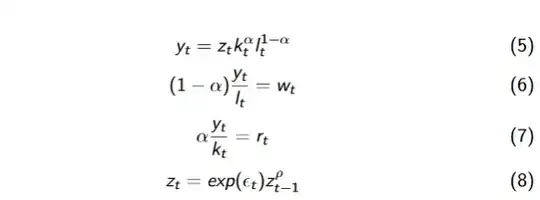
    My recommendation is to avoid directly transcribing math into MA code. Try to adapt to MA programing paradigm. For instance the following object y[a,b][c,d][x] could denote a function with 2 sup and 2 superscripts and one variable. – yarchik Jun 30 '19 at 07:58
  • 6
    ... and you can always use Format to define print forms, e.g. Format[y[a_, b_][c_, d_][z_]] := Subsuperscript[y, Row[{a, b}], Row[{c, d}]][z] – kglr Jun 30 '19 at 09:05
  • 3
    I think it's better to show us the specific equation system you want to code. – xzczd Jun 30 '19 at 14:43
  • I edited my question with an example model of non-linear equations. If I find a way to Code models of this kind efficiently, it will be a real contribution to using Mathematica for modeling non-linear systems. – Tugrul Temel Jul 02 '19 at 05:38
  • 1
    Are the $k$ in $R_{k, t+1}$ and the $k$ in $k_t$ the same? – xzczd Jul 02 '19 at 05:50
  • 1
    Is t time? Is this a system of difference equations? – Chris K Jul 02 '19 at 05:51
  • @Chris K: t is time and it can be thought as a system of difference equations. My question is not about solving the model but writing the system equations most efficiently using Mathematica. k and k subscript t is the same variable. No subscript means current time t. – Tugrul Temel Jul 02 '19 at 05:56
  • 2
    Well, my experience is, the best way to code an equation system is (at least partly) determined by subsequent solving process. Another question: do the superscript always mean Power in the system? – xzczd Jul 02 '19 at 06:13
  • @xzczd: You touched upon an important point. Superscripts of variables should only refer to location or position of the variables, has nothing to do with mathematical operations like square or square root etc. Power should be treated separately. My question ultimately boils down to ask: Is Mathematica an efficient programming language for solving a large system of dynamic non-linear equations with many superscripts and subscripts and powers...? – Tugrul Temel Jul 02 '19 at 06:45
  • Then I think it's better to follow the suggestion from @yarchik , unless your system is so complicated that notations like y[a,b][c,d][x] are too hard to read and check. – xzczd Jul 02 '19 at 06:57
  • @xzczd: Yes, my notations are complex and that is why I consulted this forum to have an efficient coding methods. I still do not beleiv that Mathematica cannot handle modeling of the complex non-linear equations system. Simply I cannot beleiv that is true. – Tugrul Temel Jul 02 '19 at 07:17
  • Still, I think it's better to talk a bit about how you'll solve the system. There're ways to code this system in 2D form efficiently. (At least more efficient than directly typing Superscript[…] and press Ctrl+Shift+N. ) But they may not be convenient for certain subsequent processing. – xzczd Jul 02 '19 at 07:29
  • 1
    If you want to use built-in functionality for solving difference equations (RecurrenceTable) to solve your system, you will have to use Mathematica notation: k[t] not k_t. – Chris K Jul 02 '19 at 07:38
  • 2
    @ChrisK Subscript can be used in this case actually: RecurrenceTable[{Subscript[a, n + 1] == 3 Subscript[a, n], Subscript[a, 1] == 7}, Subscript[a, n], {n, 1, 10}] – xzczd Jul 02 '19 at 07:46
  • @xzczd Huh, that's a new one for me. Interesting! I thought RecurrenceTable was basically a discrete-time clone of NDSolve. – Chris K Jul 02 '19 at 07:51
  • @ChrisK It's OK to use it in NDSolve, too: `s = NDSolve[{D[Subscript[y, x], x] == Subscript[y, x] Cos[x + Subscript[y, x]], Subscript[y, 0] == 1}, Subscript[y, x], {x, 0, 30}];

    Plot[Evaluate[Subscript[y, x] /. s], {x, 0, 30}, PlotRange -> All]` :D

     – xzczd Jul 02 '19 at 07:59
  • 1
    @xzczd Yeah, I expected that would turn out to be the case as soon as I made my last comment. That's pretty ugly, but the RecurrenceTable actually looks nice. – Chris K Jul 02 '19 at 08:07
  • 1
    If the only issue here is just typing Superscript in an easy way, you'll find this post interesting: https://mathematica.stackexchange.com/a/57492/1871 – xzczd Jul 02 '19 at 08:28
  • 1
    According to the answer below, your problem is completely solved by the solution given in my last comment, isn't it? – xzczd Jul 04 '19 at 06:33
  • 1
    Possible duplicate of Preventing Superscript from being interpreted as Power when using Ctrl+^ shortcut? – xzczd Jul 04 '19 at 06:36
  • @xzczd: Yes, of course, your answer helped me. The answer I gave below is in fact a duplicate of the info given in the link you provided. However, with a simple example I showed the fine difference between subscript and power notations in the same equation. I think my answer with an example is useful for those who are not very technical. Thanks. – Tugrul Temel Jul 05 '19 at 07:12

1 Answers1

1

I have found out an answer to my questions: 1) how to typeset mathematical equations in the text-book format, and 2) how to differentiate superscripts from power notation.

My answer to question (1) is taken from this forum. To write an equation with superscripts and power at the same time, run the following Code once in the beginning of your program:

AppendTo[
CurrentValue[$FrontEnd, "InputAliases"], 
"sps" -> TemplateBox[{"\[SelectionPlaceholder]", "\[Placeholder]"}, 
"Superscript"]
];

Then enter Esc sps Esc to write an equation with pure superscript notation, and then use Built-in MMA pallate for power notation Ctrl+^. This will create a math equation or notation with superscript combined with power notation.

To answer question (2), I give an example of creating a math notation with pure power. Just looking at the following example should be sufficient to see that in the first math notation, pure superscripts are combined with power 2, and in the second math notation using the MMA pallate Ctrl+^ is used to create pure power notation. Using these two different notations in typesetting math equations is so powerful and makes our life very easy.

Thank you all commenting on my question and especially the MMA links provided by some of the comments given.

enter image description here

Tugrul Temel
  • 6,193
  • 3
  • 12
  • 32