0

I'm trying to reproduce a paper. The point is that I have three variables and I will like to do the bifurcation diagram.The paper is this one:"A chaotic model of migraine headache considering the dynamical transitions of this cyclic disease" by Atiyeh Bayani, Sajad Jafari,Boshra Hatef and Julien Clinton.If you want to check it all. I'll show you the model in wich all the parameters are fixed except (e01) which is going to be my bifurcation parameter.Any idea? enter image description here 

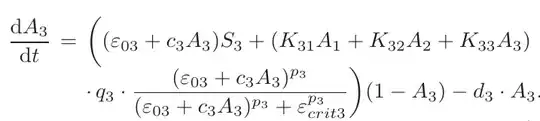
A1dot[A1_, e01_, A2_, 
   A3_] := ((e01 + c1*A1)*
       s1 + (K11*A1 + K12*A2 + K13*A3)*
       q1*((e01 + c1*A1)^
           p1/((e01 + c1*A1)^
            p1) + ecrit1^p1))*(1 - A1) - (d1*A1);
A2dot[A1_, A2_, 
   A3_] := ((e02 + c2*A2)*
       s2 + (K12*A1 + K22*A2 + K23*A3)*
       q2*((e02 + c2*A2)^
           p2/((e02 + c2*A2)^
            p2) + ecrit2^p2))*(1 - A2) - (d2*A2);
A3dot[A1_, A2_, 
   A3_] := ((e03 + c3*A3)*
       s3 + (K31*A1 + K32*A2 + K33*A3)*
       q3*((e03 + c3*A3)^
           p3/((e03 + c3*A3)^
            p3) + ecrit3^p3))*(1 - A3) - (d3*A3);
Valentina Bedoya
  • 1
  • 1
  • 1
    Please edit your question to include the Mathematica code for the equations. Also include any constraints/assumptions for the parameters/variables. – Bob Hanlon Jul 16 '19 at 00:28
  • "all the parameters are fixed except (e01)" -- Edit the question to include the specific fixed values of the parameters. – Bob Hanlon Jul 16 '19 at 01:27
  • I'm sorry!. I totally forgot to write the values of the parameters. For the other side, I'm not completely sure about the constraints, probably you could look at the section "Numerical results and discussion" on the paper because I'm a little bit lost with their procedure and I can't find an explicit constraint. Just the values of A [0,1] and all the parameters values. – Valentina Bedoya Jul 16 '19 at 02:14
  • c1 = 1; s1 = 0.1; K11 = 0; K12 = -1; K13 = -7; q1 = 1; p1 = 4; ecrit1 = 1; d1 = 0.1; e02 = 1; c2 = 1; s2 = 0.1; K21 = 0; K22 = -1; K23 = -7; q2 = 1; p2 = 4; ecrit2 = 1; d2 = 0.1;

    e03 = 1; c3 = 1; s3 = 0.1; K31 = 0; K32 = -1; K33 = -7; q3 = 1; p3 = 4; ecrit3 = 1; d3 = 0.1;

     – Valentina Bedoya Jul 16 '19 at 02:18
  • @ValentinaBedoya I did not find the chaotic modes that are indicated in the article with parameters they used. Your parameters and parameters in the article are different. Why? – Alex Trounev Jul 16 '19 at 05:44
  • 1
    Could you please add the equations in Mathematica form? – Chris K Jul 16 '19 at 06:43
  • You're right. My mistake this is theirs.c1 = 1; s1 = 0.1; K11 = 0; K12 = -1; K13 = -7; q1 = 1; p1 = 4; ecrit1 = 1; d1 = 0.1; e02 = 1; c2 = 1; s2 = 0.1; K21 = 1; K22 = 0; K23 = 0; q2 = 1; p2 = 4; ecrit2 = 1; d2 = 0.1;

    e03 = 1; c3 = 1; s3 = 0.1; K31 = 23; K32 = 0; K33 = 0; q3 = 1; p3 = 4; ecrit3 = 1; d3 = 0.1;

     – Valentina Bedoya Jul 16 '19 at 14:36
  • @AlexTrounev I'm not sure, I think they don't explain that very well. With just one unit (A1) I tried with different values of c, for example, and I think that I obtained a better behavior. So the answer is, I don't know how to obtain that with all the units (A1,A2,A3) :( – Valentina Bedoya Jul 16 '19 at 23:04
  • @ValentinaBedoya I did not find chaotic modes either. Here's a copy of my notebook. It includes a few Mathematica tips for nicely formatting things. – Andrew Norton Jul 17 '19 at 07:59
  • @AndrewNortonThank you so much for your help, I just check your notebook, I was wondering if maybe you could explain to me a little bit what your plots mean. – Valentina Bedoya Jul 17 '19 at 12:44
  • You're welcome. I was just messing about... from what I could make out from the PDF, it seemed like they wanted to plot Variance[{A1,A2,A3}] against e01, and (I think?) you're suppose to do that for t -> Infinity (eg. tmax=100). If there was any chaos, then I think the values A1[Infinity] etc. are suppose to scatter all over the place as e01 varies, but instead they change smoothly with e01 and make curves instead of scatter plots. – Andrew Norton Jul 18 '19 at 13:52

0 Answers0