RecursionLimit errors on Manipulate a DensityPlot expression

Question

I am trying to do an interactive visualization of a very simple neural network (inspired by tensorflow playground):

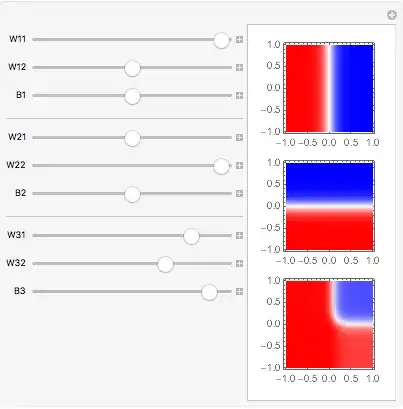
Manipulate[
 N1 = (1/(1 + Exp[-(W11 x + W12 y - B1)]));
 N2 = (1/(1 + Exp[-(W21 x + W22 y - B2)]));
 N3 = (1/(1 + Exp[-(W31 N1 + W32 N2 - B3)]));
 PP[expr_] := DensityPlot[expr, {x, -1, 1}, {y, -1, 1},
   ColorFunction -> 
     (If[# > 0.5, Lighter[Blue, -2 # + 2], Lighter[Red, 2 #]] &),
   ColorFunctionScaling -> False,
   MaxRecursion -> 2, 
   WorkingPrecision -> MachinePrecision];
 Column[{PP[N1], PP[N2], PP[N3]}],
 {{W11, 10}, -10, 10}, {{W12, 0}, -10, 10}, {{B1, 0}, -10, 10},
 Delimiter,
 {{W21, 0}, -10, 10}, {{W22, 10}, -10, 10}, {{B2, 0}, -10,  10},
 Delimiter,
 {{W31, 5}, -10, 10}, {{W32, 5}, -10, 10}, {{B3, 8}, -10, 10}]

It kind of works. However, I get a lot of RecursionLimit ($RecursionLimit::reclim2) errors while I manipulating the sliders. They seem to come from the plotting function, but I am not sure I understand why, since the function I am plotting it is not really recursive.

If there is a better write way to write this visualization (I am new to Mathematica) please let me know in the comments.

Answer 1

This seems to work. I changed it around to the way I tend to do things before seeing about errors: I put the definition of PP[] outside Manipulate; it needs to be defined only once. I replaced the global variables N1, N2, N3 with With[] statements. It seems asking for trouble to have a Manipulate depend on global variables (for instance, see here and here). Indeed the changes to N1 etc. cause a dynamic update, and when that update assigns values to N1 etc, it triggers another update, and so on ad infinitum. You can tell you're in such an infinite loop because the cell bracket stays highlighted or flickers between highlighted and unhighlighted. The only other advice is to not start your symbol names with a capital letter, but I made no changes in that regard.

PP[expr_] := 
  DensityPlot[expr, {x, -1, 1}, {y, -1, 1}, 
   ColorFunction -> (If[# > 0.5, Lighter[Blue, -2 # + 2], 
       Lighter[Red, 2 #]] &), ColorFunctionScaling -> False, 
   MaxRecursion -> 2, WorkingPrecision -> MachinePrecision];

Manipulate[
 With[{
   N1 = (1/(1 + Exp[-(W11 x + W12 y - B1)])),
   N2 = (1/(1 + Exp[-(W21 x + W22 y - B2)]))},
  With[{
    N3 = (1/(1 + Exp[-(W31 N1 + W32 N2 - B3)]))
    },
   Column[{PP[N1], PP[N2], PP[N3]}]
   ]],
 {{W11, 10}, -10, 10},
 {{W12, 0}, -10, 10},
 {{B1, 0}, -10, 10},
 Delimiter,
 {{W21, 0}, -10, 10},
 {{W22, 10}, -10, 10},
 {{B2, 0}, -10, 10},
 Delimiter,
 {{W31, 5}, -10, 10},
 {{W32, 5}, -10, 10},
 {{B3, 8}, -10, 10}]