5

As the title says Im trying to build a function to compute divided difference for arbitrary list of points.

The divided difference of a set of points $\{(x_1,y_1),\ldots, (x_n,y_n)\}$ where $x_j<x_{j+1}$ is defined recursively by

$$ f[i,j]:=\frac{f[i+1,j]-f[i,j-1]}{x_j-x_i},\, f[i,i]:=y_i $$

for $j\ge i$.I tried to mimic this definition with the code

f[i_, j_, m_] := f[i, j, m] = (f[i + 1, j, m] - f[i, j - 1, m])/(
m[[j, 1]] - m[[i, 1]]) Boole[j > i] + m[[j, 2]] Boole[j == i]

where m is an arbitrary $n\times 2$ matrix. However I tried to see if this works calling f[1,1,{{1,2},{3,4}}]but it gives me a recursion limit error. How I can fix the above code? Thank you in advance.

J. M.'s missing motivation
  • 124,525
  • 11
  • 401
  • 574
Masacroso
  • 1,107
  • 5
  • 13
  • 1
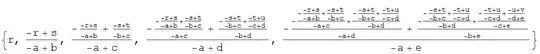
    In recursive definitions, you need to specify a one or more stopping definitions. E.g. for the factorial function f[0] = 1; f[n_] := n f[n - 1] from the docs almost works, but better is something like f[0] = 1; f[n_Integer?Positive] := n f[n - 1] or f[0] = 1; f[n_Integer] /; n > 0 := n f[n - 1] – Michael E2 Jul 27 '19 at 12:11
  • @MichaelE2 but these stops are already defined in the function, when you can something where $j=i$ – Masacroso Jul 27 '19 at 12:20
  • 2
    FWIW, here's a procedural def. based on the algorithm in Atkinson, Intro. to Num. Anal.: dividedDifference[x_, f_] := Module[{d}, With[{n = Length[(x)]}, d = f; (* div. diff. computed in place *) Do[ d[[j]] = (d[[j]] - d[[j - 1]])/(x[[j]] - x[[j - k + 1]]), {k, 2, n}, {j, n, k, -1}]; d ]] -- x is a list of nodes and f a list of values at the nodes. For input m, the call should be dividedDifference @@ Transpose@m. – Michael E2 Jul 27 '19 at 12:23
  • 1
    Masacroso, you show only one definition rule for f[i_, j_, m_], which calls f[i + 1, j, m] and f[i, j - 1, m], both of which in turn call f on new arguments ad infinitum. Unless there are definition rules that you are not showing, there are no stops to this process. The calls to f will occur even if Boole[] evaluates to zero, in case you think Boole[] might stop the process. It would be possible to put the stops in using an If[] statement. – Michael E2 Jul 27 '19 at 12:28
  • @MichaelE2 OK, I thought that the Boole function would stop it, but it doesn't. I will try to fix it with an If statement as you said – Masacroso Jul 27 '19 at 12:30
  • 1
    @Michael's implementation is in fact a triangular recursion, and is really the most efficient method to build up the divided difference table. – J. M.'s missing motivation Jul 28 '19 at 02:50

2 Answers2

8

Well, instead of evaluating an individual entry as $ f_{ij} $ once at a time, here I provide an implementation generating the whole upper-triangular $ f $ matrix. So here we go:

Clear[fmat]
fmat[pts : {{_, _} ..}] := Module[{n = Length[pts], kernels, xs, ys, denomenators, entries},
                                  {xs, ys} = pts\[Transpose]; 
                                  kernels = NestList[Insert[#, 0, 2] &, {-1, 1}, n - 2];
                                  denomenators = ListCorrelate[#, xs] & /@ kernels;
                                  entries = FoldList[Differences[#]/#2 &, ys, denomenators];
                                  SparseArray[MapIndexed[Band[Prepend[#2, 1]] -> # &, entries], n]
                                 ]

To check its validity, one can see a symbolic result and compare it with that on the Wiki page:

enter image description here

Then below calculation is trivial

enter image description here

Also, I have tested on lists of random reals with a larger shape, say $ 1000\times 2 $. The efficiency of generating the $ 1000\times 1000 $ $ f $ matrix is acceptable, at least.

P.S. I learnt that the calculation of divided difference is related to Newton interpolation. So if your purpose is to do so interpolations, you can directly use built-in functions like Interpolation, InterpolatingPolynomial, etc.

Αλέξανδρος Ζεγγ
  • 9,783
  • 3
  • 20
  • 41
4
ClearAll[dividedDif]
dividedDif = NestList[#/(#[[1, 1]] + #[[-1, -1]] &[Denominator /@ (List @@ #)]) & /@ 
     Differences[#] &, Divide @@ (Differences /@ #), Length[#[[1]]] - 2][[All, 1 ]] &;

Prepend[dividedDif @ #, #[[1, 1]]] & @ {{r, s, t, u, v}, {a, b, c, d, e}}

enter image description here

kglr
  • 394,356
  • 18
  • 477
  • 896
  • 1
    Nice result, but I think you meant to write "dividedDif" on the last line with the Prepend. When I do that, I get the answer you show. Oddly, if you use the values {{1,2},{3,4}}, you don't get what was in the previous answer although I might have input that incorrectly. – Mark R Jul 27 '19 at 19:59
  • Thank you @MarkR. Fixed it. – kglr Jul 27 '19 at 20:00