How to vectorize this nonlinear ODE system for NDSolve?

Question

I learned a long time ago that NDSolve can often be sped up by vectorizing systems of equations. I've got a problem now that seems ideal for this approach, but I can't get it to work efficiently. Any ideas on how to speed this up? This is a simplified version of my real problem, which is orders-of-magnitude larger, but has the same issues.

There are actually two related models. The first is the master equation of a birth-death-migration-extinction stochastic process. It's linear and governed by a large transition matrix TM, which is a function of the immigration rate im.

Setting up the transition matrix:

r = 1; (* birth rate *)
k = 200; (* carrying capacity *)
e = 0.01; (* extinction rate *)
m = 0.01; (* emigration rate *)
tmax = 10^6; (* maximum time *)

SetSystemOptions["SparseArrayOptions" -> "TreatRepeatedEntries" -> Total];
SetSystemOptions["NDSolveOptions" -> "DefaultSolveTimeConstraint" -> 1200];

diagonal[vec_] := Transpose[{vec + 1, vec + 1}];
superdiagonal[vec_] := Transpose[{vec + 2, vec + 1}];
subdiagonal[vec_] := Transpose[{vec, vec + 1}];
toprow[vec_] := Transpose[{ConstantArray[1, Length[vec]], vec + 1}];

from1[n_] := -r n - r n^2/k - m n - e; (* leaving n *)
dec1[n_] := r n^2/k + m n; (* going to n-1 *)

nmax = 400; (* maximum population size *)
nrange = Range[0., nmax];

transitions = Join[diagonal[nrange], subdiagonal[Rest@nrange], superdiagonal[Most@nrange], toprow[nrange]];

TM[im_] := Module[{rates},
  rates = Join[
    from1[nrange] - im,
    dec1[Rest@nrange],
    r*Most@nrange + im,
    ConstantArray[e, nmax + 1]
  ];
  SparseArray[transitions -> rates]
];

This linear master equation for the probability p of having n individuals can be quickly solved by NDSolve in vector form for a fixed immigration rate im:

(* initial probability distribution *)
p0 = Table[If[n == Round[k], 1, 0], {n, 0, nmax}];

(* 0.03 s *)
s = NDSolve`ProcessEquations[{p'[t] == TM[0.01].p[t], p[0] == p0}, p, t][[1]];

(* 0.62 s *)
NDSolve`Iterate[s, tmax];

sol = NDSolve`ProcessSolutions[s];
ListPlot[p[tmax] /. sol, PlotRange -> All]

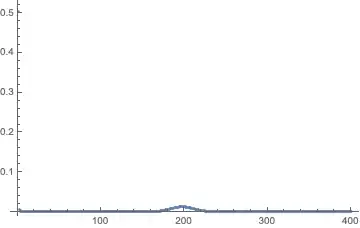
Good so far. Now the real problem: I want to make the immigration rate im a function of the probability distribution p[t] (a structured metapopulation similar to Metz & Gyllenberg 2001). This makes the system nonlinear and apparently impossible to solve efficiently in vectorized form.

First attempt:

s = NDSolve`ProcessEquations[{p'[t] == TM[m p[t].Range[0, nmax]].p[t],
  p[0] == p0}, p, t][[1]];
(* NDSolve`ProcessEquations::ndnum
  Encountered non-numerical value for a derivative at t == 0.`. *)

This seems wrong, since the initial immigration rate im=m p[0].Range[0, nmax] is in fact numerical:

m p0.Range[0, nmax]
(* 2. *)

Wrapping the SparseArray TM in Normal makes it work, but slowly:

(* 0.15 s *)
s = NDSolve`ProcessEquations[{p'[t] == Normal@TM[m p[t].Range[0, nmax]].p[t],
  p[0] == p0}, p, t][[1]];

(* 8.26 s *)
NDSolve`Iterate[s, tmax];

sol = NDSolve`ProcessSolutions[s];
ListPlot[p[tmax] /. sol, PlotRange -> All]

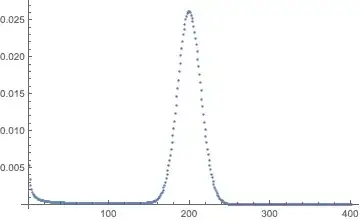
Maybe that's as good as it's going to get? No -- here are two different implementations of an unvectorized version that are faster.

First, using built-in NDSolve`ProcessEquations:

rhs = TM[m*Sum[n p[n][t], {n, 0, nmax}]].Table[p[n][t], {n, 0, nmax}];
eqns = Thread[Table[p[n]'[t], {n, 0, nmax}] == rhs];
ics = Table[p[n][0] == If[n == k, 1, 0], {n, 0, nmax}];
unks = Table[p[n], {n, 0, nmax}];

(* 2.75 s *)
s = NDSolve`ProcessEquations[Flatten[{eqns, ics}], unks, t][[1]];

(* 2.73 s *)
NDSolve`Iterate[s, tmax];

sol = NDSolve`ProcessSolutions[s];
ListPlot[Table[p[n][tmax], {n, 0, nmax}] /. sol, PlotRange -> All]
(* same output as above *)

Second, using my homemade ProcessFirstOrderODEs:

rhs = TM[m*Sum[n p[n], {n, 0, nmax}]].Table[p[n], {n, 0, nmax}];
ics = Table[If[n == k, 1, 0], {n, 0, nmax}];
unks = Table[p[n], {n, 0, nmax}];

(* 0.55 s *)
s = ProcessFirstOrderODEs[unks, rhs, ics, 0];

(* 2.82 s *)
NDSolve`Iterate[s, tmax]

sol = NDSolve`ProcessSolutions[s];
ListPlot[Table[p[n][tmax], {n, 0, nmax}] /. sol, PlotRange -> All]
(* same output as above *)

Finally, both NDSolve`Iterate stages can be sped up to around 0.6 s by processing the equations with option Jacobian -> FiniteDifference (not shown).

To recap:

• the vectorized linear problem works fine with NDSolve
• the vectorized nonlinear problem does not work with NDSolve, except when using Normal, which results in a total timing of 8.41 s
• the nonvectorized nonlinear problem with NDSolve is faster (5.48 s)
• the nonvectorized nonlinear problem with my ProcessFirstOrderODEs is even faster (3.37 s)
• the nonvectorized nonlinear problem with my ProcessFirstOrderODEs and Jacobian->FiniteDifference is fastest (1.1 s)

Questions:

• can the vectorized nonlinear problem be made to work with NDSolve without using Normal?
• is there any other way to speed up this NDSolve?

Answer 1

I think the problem is that in TM[m p[t].Range[0, nmax]], the NDSolve "variable" p[t] is incorporated into the SparseArray and protected from being assigned a value in whatever way NDSolve achieves that. This can be overcome by using _?NumericQ. This speeds up the ProcessEquations[] step and the Iterate[] step (from 9 to 4 sec.). Specifying Method -> "StiffnessSwitching" speeds up Iterate[] even more. (For some reason, it does not speed up the OP's fastest way, with ProcessFirstOrderODEs.)

ClearAll[TM];
TM[im_?NumericQ] := 
  Module[{rates}, 
   rates = Join[from1[nrange] - im, dec1[Rest@nrange], 
     r*Most@nrange + im, ConstantArray[e, nmax + 1]];
   SparseArray[transitions -> rates]];

s = NDSolve`ProcessEquations[{p'[t] == TM[m p[t].Range[0, nmax]].p[t],
       p[0] == p0}, p, t, 
     Method -> "StiffnessSwitching"][[1]]; // AbsoluteTiming

NDSolve`Iterate[s, tmax]; // AbsoluteTiming

sol = NDSolve`ProcessSolutions[s];
ListPlot[p[tmax] /. sol, PlotRange -> All]
(*
  {0.001504, Null}
  {1.58603, Null}
*)